第7章 统计学入门

[toc]

7.1 什么是统计学

为了回答什么是统计学，我们先要弄清楚为什么我们需要统计学。统计学的目的是对我们所处的现实世界进行解释和建模。为了做到这一点，我们需要了解总体（population）的概念。

我们将“总体”定义为某类试验、事件或模型的全体。通常情况下，“总体”是我们真正研究的对象。比如，如果我们想了解吸烟是否会导致心脏病，那么“总体”就是全世界吸烟的人群。如果我们想研究未成年人饮酒问题，那么“总体”就是所有的未成年人。

我们将“参数（parameter）”定义为描述总体某一特征的度量（数值型）。比如我们想知道所有员工（假设有1000人）中使用了违禁药品的人的比例，这个问题的结果就被称为参数。

假设我们经调查发现，1000名员工中有100人使用了违禁药品，那么违禁药品使用率等于10%，参数值就等于10%。

然而，如果员工数量超过10000人呢？我们很难追踪每一位员工的违禁药品使用情况。当遇到这种情况时，我们已经不可能直接求解参数，而只能对参数值进行估计。

为了估计参数值，我们需要从总体中抽取样本（sample）。

我们将“样本”定义为总体的子集。我们可能只调查1000名员工中的200名。假设在这200名员工中有26人使用了违禁药品，那么违禁药品使用率等于13%。请注意，13%并不是真实的参数值，因为我们并没有调查所有人！13%仅仅是我们估计的参数值。

你知道以上这个过程叫什么吗？这就是统计！

我们可以认为统计是描述总体中样本的某个特征的方法。

统计就是对参数值的估计。统计是通过研究总体子集的特征，描述总体特征的度量值。这一过程是非常有必要的，因为我们无法对地球上每一个未成年人或者吸烟者进行调查。

这就是统计学的世界——从总体中抽取样本，再对样本进行检验。所以，当你下一次再看到统计数字时请记住，它是总体中某个样本的特征，而不是总体。

7.2 如何获取数据

既然统计学研究的是总体中的样本，那么如何抽样就显得非常重要。下面我们介绍一些常用的获取数据的方法。

有两种获取分析所需数据的方法：观察法（observational）和实验法（experimental）。这两种方法各有利弊，适合不同类型的分析。

观察法

我们可以通过观察法持续记录被观测事件的特征值，但又不影响事件的发生。比如，我们通过追踪软件记录网站访客的行为习惯——在特定页面的访问时长、广告点击率等，追踪软件并不影响访客的行为。

观察法是最常见的收集数据的方法，因为它操作起来非常简单，你需要做的仅仅是观察和收集。但观察法限制了可收集的数据类型，因为作为观察者，我们对整个实验环境缺乏控制力，只能观察和收集自然发生的行为。如果我们希望主动诱发某种行为并进行观察，那可能并不适合使用观察法。

实验法

实验法包含一组实验方法和实验对象的反映，实验对象也被称为实验单元。大部分科学实验均使用实验法收集数据。实验组织者将人群分为两组或多组（通常是两组），其中一组为实验组（experimental group），另一组为对照组/控制组（control group）。

对照组暴露在特定环境中并被仔细观察。与此同时，实验组暴露在另一个不同的环境中并被仔细观察。实验组织者将两组数据对比分析后，决定哪个实验环境更加有利。

在市场营销活动中，假设我们让一半用户使用经过特殊设计的登录页面（网页A），然后统计这些用户是否进行了注册。同时，我们让另一半用户使用不同的登录页面（网页 B），然后统计这些用户是否进行了注册。通过对比两个页面的注册率，我们可以决定哪个网页的表现更好，然后进行推广。这种方法叫作A/B测试。

下面我们用Python演示具体的案例。假设某项A/B测试获得的数据如下：

1
results=[['A',1],['B',1],['A',0],['A',0]...]

在results列表中，列表的每个对象表示一个用户，每个用户有以下两个特征：

  • 登录网站的页面，用字母A或B表示；
  • 是否完成了注册（0表示否，1表示是）。

我们可以对原始数据进行聚合，得到以下两组数据：

1
2
3
users_exposed_to_A=[]
users_exposed_to_B=[]
#create two lists to hold the results of each individual website

创建了以上两个列表后，就可以存储用户注册情况的布尔型统计结果。我们对所有的测试结果进行迭代，将每个结果分派到相应的类别中，如下所示：

1
2
3
4
5
6
for website,converted in results:#iterate through the results
    #will look something like website=='A' and converted==0
    if website=='A':
        users_exposed_to_A.append(converted)
    elif website=='B':
        users_exposed_to_B.append(converted)

现在，每个列表都包含了若干个1和0。

请记住，1表示用户在访问了网页后进行了注册。0表示用户在访问了网页后，直接离开，没有进行注册。

为了计算网页的访问用户数，我们使用Python的len()方法，如下所示：

1
2
len(users_exposed_to_A)==188 #number of people exposed to website A
len(users_exposed_to_B)==48 #number of people exposed to website B

为了计算注册用户数，我们使用Python的sum()方法，如下所示：

1
2
sum(users_exposed_to_A)==54 #people converted from website A
sum(users_exposed_to_B)==48 #people converted from website B

1和0相加等于1，那么sum的结果即为1的数量总和。

我们用列表的长度（总用户数）减去列表元素之和（注册用户数），得到的是没有注册的用户数，如下所示：

1
2
3
4
len(users_exposed_to_A)-sum(users_exposed_to_A)==134
#did not convert from website A
len(users_exposed_to_B)-sum(users_exposed_to_B)==110
#did not convert from website B

对上述统计结果进行整理和汇总后，我们得到了A/B测试的结果。

未注册 注册
网页A 134 54
网页B 110 48

我们可以快速计算每个网页的转化率：

  • 网页A的转化率：54/(134+54)=0.288
  • 网页B的转化率：48/(110+48)=0.300

网页A和B的转化率确实有所不同，但差异不大。网页B的转化率看起来高于A，我们是否可以认为网页B的转化率显著高于网页A呢？不可以！为了得到A/B测试的统计显著性（statistical significance），我们需要对其进行假设检验。在下一章，我们将对各种假设检验方法进行详细介绍，也会采用最合适的假设检验方法继续研究本案例。

7.3 数据抽样

统计指标体现的是总体中某个样本的特征值。接下来，我们将介绍两种最常见的数据抽样方法：概率抽样和随机抽样。我们将重点讨论随机抽样，因为它是最常用的决定样本大小和数据的抽样方法。

7.3.1 概率抽样

概率抽样（probability sampling）指总体中每个元素以给定的概率被抽中。每个元素被抽中的概率既可以相等，也可以不相等。最简单也是最常见的概率抽样方法是随机抽样（random sampling）。

7.3.2 随机抽样

假设我们正在进行A/B测试，希望将用户分为A组和B组。以下是3个分组建议：

  • 根据用户地址进行分类。西海岸的用户归为A组，东海岸的用户归为B组。
  • 根据用户访问网站时间进行分类。晚上7点至早上4点的用户归为A组，其余用户归为B组。
  • 完全随机分类。每个新用户按照50/50的比率，平均分到A组和B组。

前两种方法确实可以对用户进行分组，也容易实施。但是它们有一个根本的缺陷——面临样本偏差（sampling bias）的风险。

当抽取样本的方式对分析结果具有较大影响时，我们称存在样本偏差。

我们很容易解释为什么建议1和建议2面临样本偏差风险。当我们按照用户的地理位置或者登录时间进行分类时，我们在实验中引入了干扰因子（confounding factor），导致我们对实验结果缺乏掌控力，这可不是一个好消息！

干扰因子指间接影响实验结果的隐性变量。简单理解，干扰因子是未被作为分析对象，但却影响着分析结果的变量。

由于抽样方式不科学不合理，实际上隐性变量z被引入到了实验中。

在本例中，第1种分类方法没有考虑到地理因素对A/B测试结果的潜在影响。比如，如果网页A本身就对西海岸用户没有吸引力，那么西海岸这个地理位置将影响测试结果，导致我们无法区分A/B测试结果是由用户地理位置造成的，还是网站本身造成的。

同样地，第2种分类方法可能引入的干扰因子是时间。比如，网页B在夜间环境的使用效果较好（网页A则恰恰相反），导致用户离开网站A仅仅是因为访问的时间不合适。这些都是我们需要避免的影响因子。因此，我们使用第3种抽样方式——完全随机。

建议1和建议2都会导致样本偏差，因为我们错误地选择了样本，引入了干扰因子，导致有不可控的变量影响实验结果。

换句话说，根据控制变量法，我们希望只有一个变量（本例中即网页设计样式）来影响结果。第1种分类方法多引入了一个地理变量，第2类分类方法多引入了一个时间变量。

随机抽样指总体中每一个元素被抽中的机会是相等的。这是决定样本组成最简单实用的方法。在随机抽样中，总体中的每个元素都有相同的概率成为样本的一员，所以有效避免了引入干扰因子。

7.3.3 不等概率抽样

等概率抽样有没有可能引起样本偏差呢？假设我们想了解员工的幸福指数，我们已经知道不可能对每位员工进行调查，因为这种办法费时、费力，不够聪明，所以我们需要抽取一个样本。数据小组推荐使用随机抽样，小组成员纷纷举手同意，因为他们认为这个方法非常聪明，听起来也符合”统计学”。然而，小组中有人提出了一个善意的疑问：“有谁知道员工的男女组成比例？”

刚才举手同意的人陷入沉默，纷纷放下举起的手。

这个问题非常重要，因为性别确实是一个干扰因子。数组小组研究后发现，公司员工中男性占比75%，女性占比25%。这意味着如果我们使用随机抽样，样本会有同样的偏倚——明显偏向男性。

为了防止出现这种情况，我们可以刻意在样本中增加女性的数量，以使样本的性别构成趋向平衡。表面上看，在随机抽样中引入偏好并不是一个好主意，但在实际应用中，轻度使用不等概率抽样，消除性别、种族、残疾等系统性偏差是非常必要且恰当的。

总而言之，等概率抽样得到的简单随机样本会降低一部分人群的声音和观点，在抽样中适当引入偏好是有必要的。

7.4 如何描述统计量

一旦我们得到了样本，就可以量化统计结果。假设我们想确定员工满意度是否和员工的薪酬高低有关，以下是一些常用的统计量。

7.4.1 测度中心

我们定义数据集的中心为测度中心（measure of center）。测度中心是对（大型）数据集进行归纳、概括，以便能够方便地进行交流的一种方式。比如，西雅图平均的降雨量和欧洲男性的平均身高都可以用对应数据集的测度中心表示。

测度中心是位于数据集“中间位置”的值。然而，不同人对“中间位置”有不同的理解。因此，测度中心有多种计算方法，以下就是其中几种计算方式。

第一种测度中心叫算术平均值（arithmetic mean）。算术平均值等于数据集中所有元素之和除以元素的个数，它是最常用的测度中心，但也有缺点。比如以下的代码；

1
2
import numpy as np
np.mean([11,15,17,14]) ==14.25

数据集的平均值是14.25，所有的数据点都非常接近平均值。但是，如果我们新增一个数据点31，会发生什么变化呢？

1
np.mean([11,15,17,14,31]) ==17.6

数据集的平均值变为17.6。可见，新增加的数据点对数据集的平均值产生了较大影响。这是因为算术平均值对离群值（outliers）非常敏感。31几乎是数据集中其他值的两倍，因此它使平均值发生了较大变化。

另一个常用的测度中心是中位数（median）。中位数是已排序数据集中处于中间位置的值。

1
2
np.median([11,15,17,14]) ==14.5
np.median([11,15,17,14,31]) ==15

我们注意到，在数据集中增加31并没有对中位数产生较大影响。这是因为中位数对离群值不敏感。

简单总结，当数据集有较多离群值时，使用中位数作为测度中心比较合理。相反，如果数据集没有较多离群值，且数据点较为集中，那么使用平均值作为测度中心就是一个较好的选择。

但是，有了测度中心后，我们如何描述数据集的离散情况呢？答案是使用**变异测度(measure of variation)**。

tips:在第2章中被称为变差测度（measure of variation）

变异测度是描述数据集离散程度的指标。

7.4.2 变异测度

测度中心用于量化数据的中心，接下来我们将介绍测量数据离散程度的方法。这是识别数据集中潜在离群值的非常有效的方法。我们从一个具体案例开始。

假设我们随机抽取24个Facebook用户作为样本，并统计他们的Facebook好友数。整理后的数据如下：

1
2
friends=[109,1017,1127,418,625,957,89,950,946,797,981,125,455,731,1640,485,1309,472,1132,1773,906,531,742,621]
np.mean(friends) ==789.1

列表的平均值是789。因此根据此样本，我们可以认为每个Facebook用户平均拥有的好友数量是789个。但是，在那些有89个好友或者1600个好友的人看来，这个数字并不合理。事实上，只有极个别用户的好友数接近789。

既然这样，那我们试试中位数，因为中位数不会受离群值的影响，如下所示：

1
np.median(friends) ==769.5

列表的中位数是769.5，非常接近平均值。虽然用中位数代替平均值的想法很不错，但遗憾的是中位数仍然无法体现数据点之间的巨大差异。事实上，统计学家专门用变异测度衡量数据点之间的差异。最简单的变异测度是区间（range）。区间等于数据集最大值减去最小值，如下所示：

1
np.max(friends)-np.min(friends)=1684

区间量化了两个极值（最大值和最小值）之间的距离。实际上，区间在实践中的应用场景较少，但仍有其重要作用。比如在涉及科学测量和安全测量的场景之中，我们可能会非常关心离群值的离散程度。

假设汽车厂商希望测量安全气囊打开所花费的时间。虽然也可以用平均值进行衡量，但汽车厂商同样关心安全气囊打开所需的最长时间和最短时间，因为这意味着生和死的区别！

回到Facebook案例中，我们已经知道数据集的区间是1684，但我们仍不确定它是不是描述数据分散程度的最好指标。下面，我们将介绍最常用的变异测度——**标准差(standard deviation)**。

我相信很多人都曾听过标准差，有些人甚至对这个词有一定程度的恐惧感。标准差究竟意味着什么呢？当我们分析总体的某个样本时，标准差（用符号s表示）用于量化数据点偏离样本算术平均值的程度。

标准差其实是描述数据分散程度的一种指标。计算标准差的通用公式是：
$$
s=\sqrt{∑(x-\bar x)^2 \over n-1}
$$
其中：

  • s是样本的标准差；
  • x是样本的数据点；
  • $\bar x$是样本的均值；
  • n是样本所含数据点的数量。

在你被公式搞糊涂之前，我先对标准差公式进行讲解。我们先用样本中的每一个值减去样本的算术平均值，再将所有的差值分别平方后相加，然后除以样本数据点的数量n，最后开平方，即可得到样本的标准差。

除了分析标准差公式之外，我们还可以这样理解标准差。标准差公式派生于距离公式，因此，标准差本质上是计算数据点和算术平均值之间某种平均距离的公式。

我们再次仔细观察标准差公式，你会发现这是有道理的。

（1）x-$\bar x$，我们得到数据点和样本均值的差异；

（2）$(x-\bar x)^2$ ，我们为离群值赋予了更多权重，因为平方让差异变得更大；

（3）对上一步得到的值相加后除以样本元素数量n，我们得到了每个数据点和样本均值的平均平方距离；

（4）对上一步得到的值开平方，我们将结果转化为能够接受的尺度。因为我们在第2步将数据尺度变成了好友数的平方，对结果开平方后，又让数据尺度恢复到了和之前一致的尺度。

回到Facebook案例，我们借助图形进行可视化的讲解。首先从计算标准差入手。我们已经知道数据集的算术平均值是789，所以将789作为计算标准差的均值。

我们首先计算每个数据点和均值的差，先各自平方后相加，再除以某个很小的数值，最后开平方。计算过程如下：
$$
s=\sqrt{(109-789)^2+(1017-789)^2+…+(621-789)^2 \over24}
$$
我们也可以用Python编程计算（效率更高）。

1
np.std(friends) #==425.2

425表示样本数据的离散程度。换言之，我们可以认为425是每个数据点和均值间的平均距离。显然，样本数据非常分散！大家拥有的Facebook好友数量并不接近某个值——包括均值。

下面我们用条形图可视化展示样本数据、均值和标准差，以便更清晰地观察样本特征。如图所示，每个柱子表示一个用户，柱子的高度表示该用户的好友数量。

1
2
3
4
5
6
7
8
import matplotlib.pyplot as plt
y_pos=range(len(friends))

plt.bar(y_pos,friends)
plt.plot((0,25),(789,789),'b-')
plt.plot((0,25),(789+425,789+425),'g-')
plt.plot((0,25),(789-425,789-425),'r-')
plt.show()

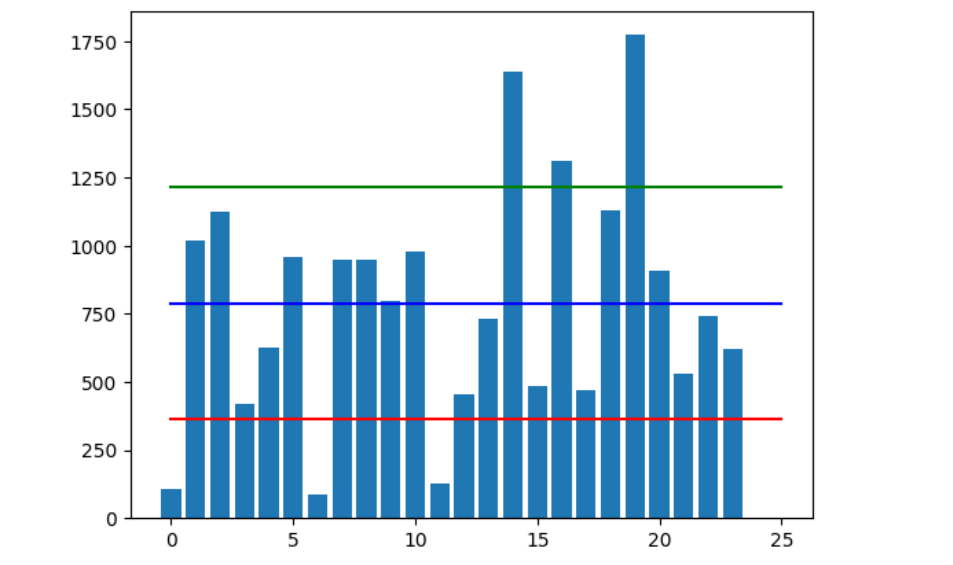
image-20230407102128522

图中蓝色横线为均值（789），红色横线为均值减去标准差（789-425=364），绿色横线为均值加上标准差（789+425=1214）。

我们注意到图中大部分柱子都位于绿色横线和红色横线之间，离群值则在该区域之外，其中位于红色横线下方和绿色横线上方的离群值各有3个。

需要强调的是标准差的单位和数据集本身的单位是一致的。所以，我们可以认为Facebook好友数的标准差是425个好友。

另一种变异测度是之前介绍过的方差，方差和标准差的区别在于是否平方。

标准差和方差都可以衡量数据集的分散程度，它们和测度中心一起，构成了一组描述数据集特征的指标。但是，如果我们想比较两个不同数据集，甚至数据尺度完全不同的两个数据集的离散程度，该怎么办呢？此时就需要使用变异系数（coefficient of variation）。

7.4.3 变异系数

变异系数是样本标准差除以样本均值得到的比率。

通过该比率，我们可以对标准差进行标准化，从而对多个数据集进行横向比较。我们经常用这个指标对比数据尺度不同的样本的均值和分布情况。

案例：员工薪酬

当我们试图对比不同部门员工薪酬的标准差和均值时，很容易发现，很难直接进行对比！比如表7.2，Mailroom 部门平均薪酬是25000美元，Executive部门平均薪酬是124000美元，两者相差了一个数量级。

部门 平均薪资 标准差 变异系数
Mailroom $25000 $2000 8.0%
Human Resources $52000 $7000 13.5%
Executive $124000 $42000 33.9%

但是，通过最后一列变异系数我们可以发现，虽然Executive部门的人均薪酬较高，但薪酬差异也最大。这很可能是因为CEO的薪酬远远高于普通管理人员——虽然他们也属于管理部门，但是导致数据分布较广。反过来，虽然Mailroom部门的平均薪酬并不太高，但变异系数只有8%，说明部门员工间的薪酬相差不大。

总之，通过变异测度，我们可以研究数据集更多的特征，找出能够包含大部分数据点的合理区间。

7.4.4 相对位置测度

我们可以将测度中心和变异测度结合在一起，生成相对位置测度（measure of relative standing）。相对位置测度用于度量数据点相对于整个数据集的位置。下面我们要学习统计学中最重要的统计量之一：z分数（z-score）。

z分数实例

跳转锚点2

z分数用于描述单个数据点和均值之间的距离。数据点x的z分数计算方法如下：
$$
z={x-\bar x\over s}
$$
其中：

  • x是样本中的数据点；
  • $\bar x$是样本均值；
  • s是样本标准差。

我们曾说，标准差近似于数据点和均值之间的平均距离。那么现在，z分数则是每个数据点到均值的距离。z分数是标准化后的数据点到均值的距离，数据点减去均值，再除以标准差即可得到z分数。

在统计学中，我们经常使用z分数，它是将不同尺度数据正态化的一种非常重要的方式。下面我们用z分数对Facebook好友案例进行标准化。我们将通过以上公式计算每个用户的z分数，如下所示：

1
2
3
4
5
6
7
8
z_scores=[]
m=np.mean(friends) # average friends on Facebook
s=np.std(friends)  # standard deviation friends on Facebook

for friend in friends:
    z=(friend-m)/s #z-score
    z_scores.append(z) #make a list of the scores for plotting
plt.bar(y_pos,z_scores)

下图是使用z分数做成的柱形图，其中每一个柱子代表一个用户，柱子的高度由之前的好友数替换为对应的z分数。我们可以发现：

  • 图中有负值（意味着数据点位于均值下方）；
  • 柱子的高度不再表示好友数，而是好友数和均值的差异程度。

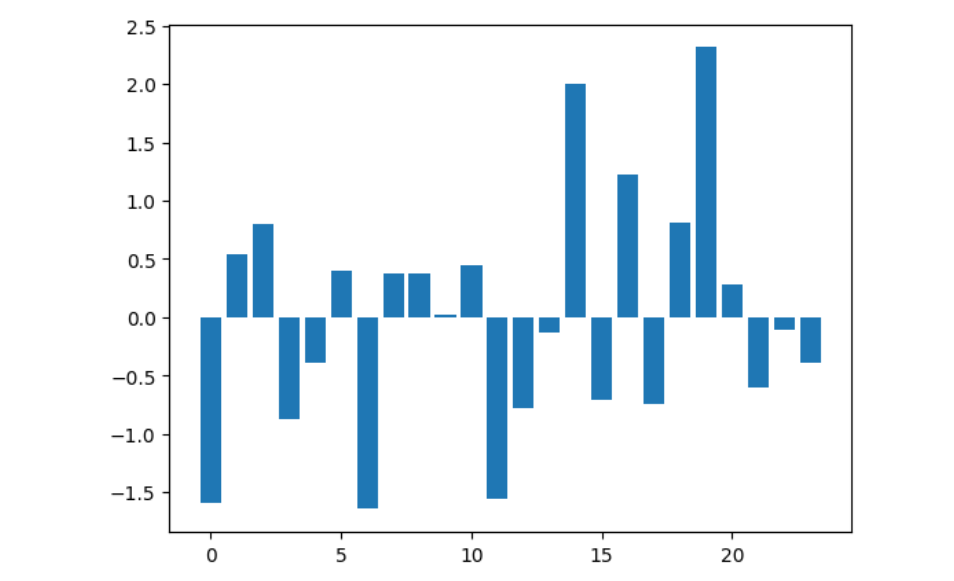
image-20230407210443217

同时，通过上图，我们可以非常快速地找出好友数比平均值多或少的人。比如，横坐标0对应的人拥有的好友数低于平均值（他/她只有109个好友，均值是789个）。我们之前曾绘制了3条辅助线：一条均值线，一条均值加标准差，一条均值减标准差。当我们将这些值加入到z分数公式会出现：

$\bar x$ 的z分数=$\bar x-\bar x\over s$=$0\over s$=0

$\bar x$ +s的z分数=$(\bar x+s)-\bar x \over s$=$s\over s$=1

$\bar x$ -s的z分数=$(\bar x-s)-\bar x \over s$=$-s\over s$=-1

这不是巧合！当我们用z分数方法对数据集进行标准化时都会出现这种情况。下面我们在图中加入3条辅助线：

1
2
3
4
plt.bar(y_pos,z_scores)
plt.plot((0,25),(1,1),'g-')
plt.plot((0,25),(0,0),'b-')
plt.plot((0,25),(-1,-1),'r-')

如图所示，上面的代码在图形中增加了3条横线：

  • 蓝色横线（y=0）表示和均值相差0个标准差；
  • 绿色横线指比均值高1个标准差；
  • 红色横线指比均值低1个标准差；

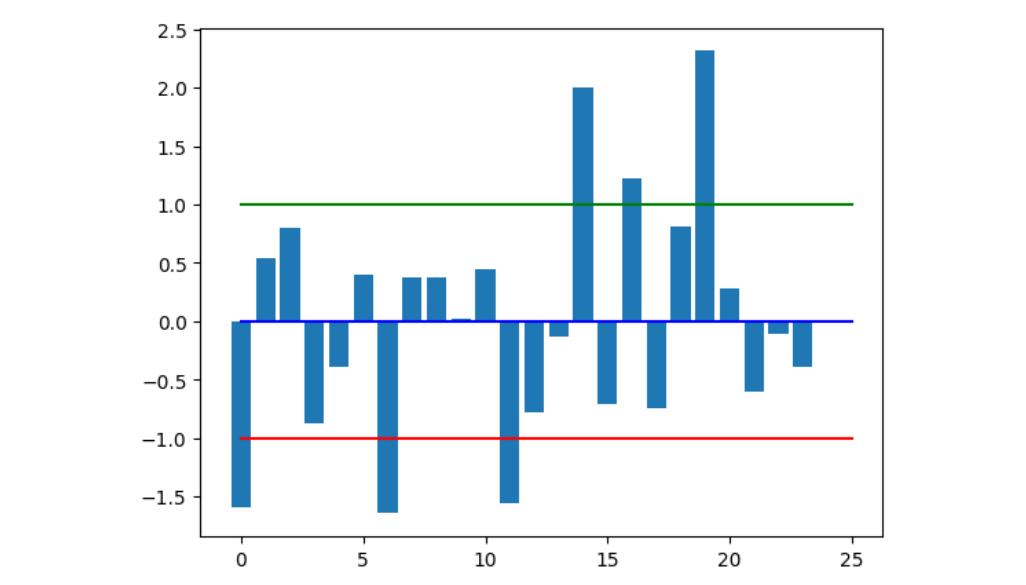
image-20230407211551006

3条横线在图中的相对位置和使用好友数绘制的图形非常相似。仔细观察不难发现，高于绿色横线和低于红色横线的还是之前那6个用户。

  • 位于红色横线之下和绿色横线之上的人，和均值的差异超过一个标准差；
  • 位于红色横线和绿色横线之间的人，和均值的差异低于一个标准差。

z分数是对数据标准化的重要方法，这意味着我们可以将整个数据集转换为同一尺度。比如，对于Facebook案例中出现的用户，假设我们有他们的幸福指数（介于0～1），数据如下：

1
2
3
4
5
6
friends=[109,1017,1127,418,625,957,89,950,946,797,981,125,455,731,1640,485,1309,472,1132,1773,906,531,742,621]
happiness=[.8,.6,.3,.6,.6,.4,.8,.5,.4,.3,.3,.6,.2,.8,1,.6,.2,.7,.5,.3,.1,0,.3,1]
import pandas as pd

df=pd.DataFrame({'friends':friends,'happiness':happiness})
df.head()

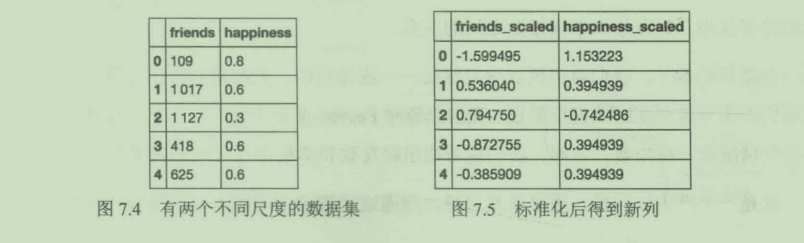
数据集有两个不同尺度的列，friends列最大值超过1000，happiness列值则介于0~1。

为了解决这一差异，我们使用scikit-learn内置的数据预处理包对数据集进行简单的标准化，如下所示：

1
2
3
4
5
from sklearn import preprocessing

df_scaled=pd.DataFrame(preprocessing.scale(df),columns=['friends_scaled','happiness_scaled'])

df_scaled.head()

以上代码将friends和happiness列同时压缩到相同尺度。sklearn的preprocessing模块在执行过程中，对每一列分别执行以下操作：

（1）计算该列的均值；

（2）计算该列的标准差；

（3）对该列每个元素进行z分数标准化。

代码运行后得到两列处于相同尺度的新列。如图7.5所示。

image-20230408092330456

下面我们用新生成的列绘制散点图。

1
df_scaled.plot(kind='scatter',x='friends_scaled',y='happiness_scaled')

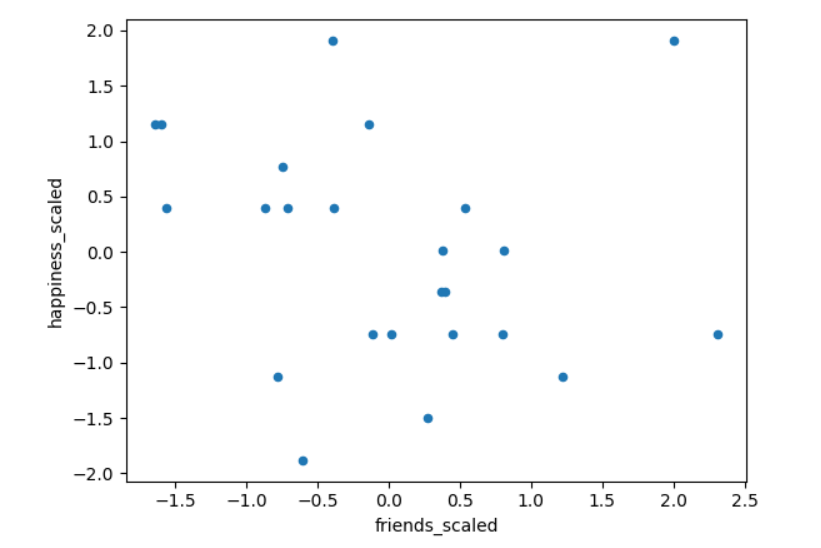
image-20230408092858358

通过z分数将数据标准化后，我们得到了可以进一步分析的散点图。

在随后的章节，你将发现数据标准化的作用不仅仅在于提高数据的可读性，也是模型优化的必要手段之一，因为很多机器学习算法对数据尺度非常敏感，需要我们提前对数据进行标准化。

从数据中获得洞察：相关性

在本书中，我们将讨论“拥有数据”和“从数据中获得洞察”的区别。拥有数据只是成功进行数据科学过程的第一步。获取数据、清洗数据以及对数据可视化，只能帮你更好地用数据讲故事，不能揭示更深层次的问题。为了对Facebook数据做更深入的分析，我们将寻找用户好友数和幸福指数之间的关系。

在随后的章节，我们将用机器学习算法——线性回归，发掘量化特征之间的关系，但我们不需要等到那时才提出假设。我们已经对Facebook用户进行了抽样，统计了他们的社交情况和幸福指数。请问，我们能否找出好友数和幸福指数之间的关系？

这是一个严肃的问题，需要认真对待。严谨地回答这个问题需要在实验室情境下进行，但是我们可以先从提出一个假设开始。

结合已知的数据，我们有以下3种观点：

  • 好友数和幸福指数正相关（一个上升，另一个也上升）；
  • 好友数和幸福指数负相关（一个上升，另一个下降）；
  • 好友数和幸福指数没有任何相关性（一个变化，另一个基本不变）。

我们是否可以用简单的统计学知识回答以上问题呢？我认为可以。我们需要先引入一个新的概念——相关系数（correlation coefficients）。

相关系数是描述两个变量之间相关性强弱关系的量化指标。

两个数据集间的相关性描述了两者的变化关系。这一概念不仅在本例中非常重要，也是机器学习模型的核心假设之一。对于大部分预测算法，它们能够正常工作的前提是变量之间确实存在某种关系或相关性。机器学习算法通过寻找这种关系进行准确的预测。

相关系数的一些重要的内容如下。

  • 相关系数值介于-1～1。
  • 相关系数绝对值越大（接近-1或1），变量间的相关性越强。
  • 最强的相关性为-1和1。
  • 最弱的相关性为0。
  • 正相关意味着一个指标增加，另一个指标也增加。
  • 负相关意味着一个指标增加，另一个指标却下降。

我们使用Pandas快速计算各个特征之间的相关系数，如下所示：

1
2
#correlation between variables
df.corr()
friends happiness
friends 1.000000 -0.216199
happiness -0.216199 1.000000

上面的表格体现了好友数和幸福指数之间的相关性，请注意图中以下两个特征：

  • 矩阵对角线位置的单元格均为正相关（相关系数为1）。这是因为它们表示变量和变量自身的相关性，因此形成了完美的一条斜线。
  • 矩阵中对角线两边的单元格完全对称。这对任何用Pandas计算的相关性矩阵都成立。

你需要牢记一些关于相关性的告诫。首先，变量之间的相关性通常以线性关系（linear relationship）进行计算。这意味着即便变量的相关系数为零，也不能说明变量不存在任何关系，而只能说明变量间没有线性关系，变量间可能着存在非线性关系（non-linear relationship)。

另外，变量间的相关性不等同于因果关系。虽然好友数和幸福指数呈微弱的负相关性，但并不意味着好友数的增加导致了幸福指数的减少。因果关系必须通过假设验证进行确认。在随后的章节，我们将介绍具体的验证方法。

简单总结，我们可以利用相关性对变量间的关系进行假设检验，但我们还需要更多复杂的统计学方法和机器学习算法，以便对假设进行验证。

7.5 经验法则

image-20230408094018369

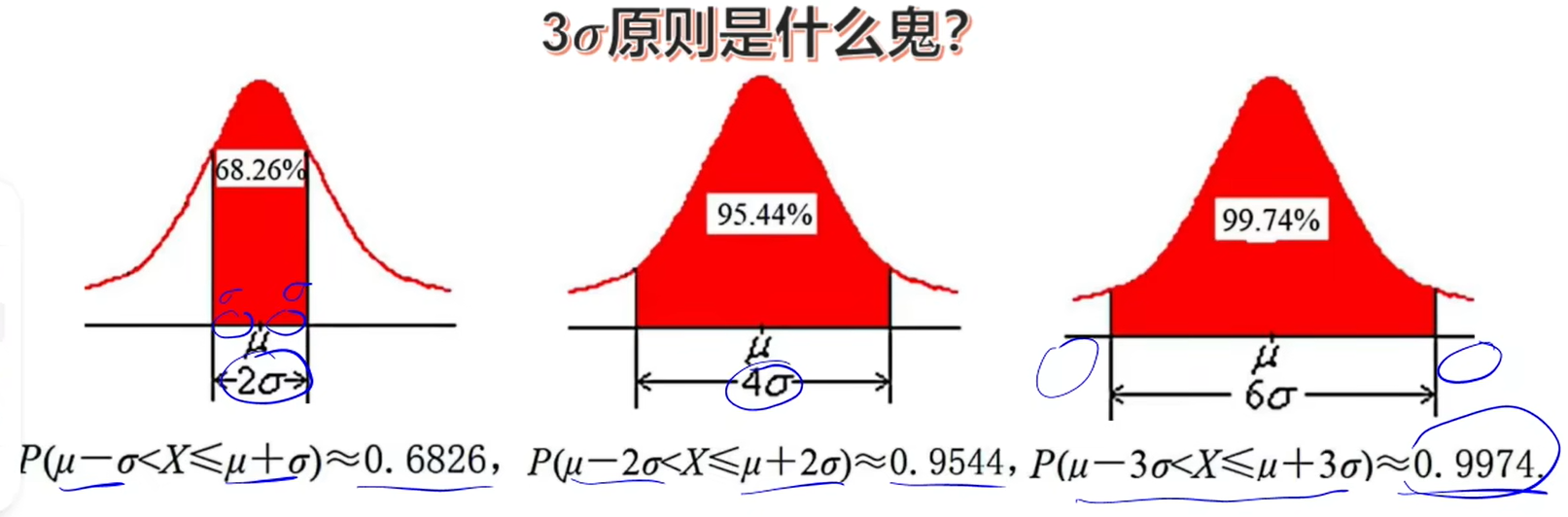
经验法则（the empirical rule）指我们可以推算出标准正态分布中每个标准差区间所含的数据量。比如根据经验法则：

  • 接近68%的数据点和均值相差1个标准差以内；
  • 接近95%的数据点和均值相差2个标准差以内；
  • 接近99.7%的数据点和均值相差3个标准差以内。

下面我们看Facebook好友数据是否具有以上特征。我们用DataFrame分别找出和均值相差1个、2个和3个标准差的百分比。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#finding the percentage of people within one standard deviation of the mean
within_1_std=df_scaled[(df_scaled['friends_scaled']<=1)&(df_scaled['friends_scaled']>=-1)].shape[0]
print(within_1_std/float(df_scaled.shape[0]))
#0.75

#finding the percentage of people within two standard deviation of the mean
within_2_std=df_scaled[(df_scaled['friends_scaled']<=2)&(df_scaled['friends_scaled']>=-2)].shape[0]
print(within_2_std/float(df_scaled.shape[0]))
#0.916

#finding the percentage of people within three standard deviation of the mean
within_3_std=df_scaled[(df_scaled['friends_scaled']<=3)&(df_scaled['friends_scaled']>=-3)].shape[0]
print(within_3_std/float(df_scaled.shape[0]))
#1.0

从计算结果可以看出，数据集并不符合经验法则。接近75%的用户和均值相差1个标准差以内，接近92%的用户和均值相差2个标准差以内，所有用户和均值的距离都不超过3个标准差。

案例：考试成绩

假设考试成绩呈正态分布，平均成绩84分，标准差6分。我们可以近似地认为：

  • 接近68%的人成绩在78~90分，因为78、90分别和84相差1个标准差；
  • 假如我们想知道成绩介于72~96分的比例，由于72、96恰好和84相差2个标准差，那么根据经验法则，接近95%的人成绩位于这个区间。

但是在现实生活中，并不是所有的数据都呈正态分布，因此经验法则并不能解决所有问题。我们有另一种理论可以帮助我们分析任何一种分布。在下一章，我们将深入研究何时可以假设数据呈正态分布，因为统计检验和假设要求源数据呈正态分布。

当我们用z分数方法对数据进行标准化时，并不要求数据呈正态分布。

正态分布

视频地址：【概率·正态分布】这是个啥玩意儿？10分钟完全入门！

image-20230408154658688

正态分布的密度函数是一个对称的图像，μ就是对称轴。

μ表示的含义是平均数。

  1. 函数的解析式是：
    $$
    \phi_{μ,σ}(x)={1\over \sqrt{2\pi}σ}·e^{-{(x-μ)^2\over2σ^2}},x∈(-∞,+∞)
    $$

  2. 服从正态分布记作X~N(μ,$$σ^2$$)，读作“X服从正态分布”

  3. 这里的μ指的就是期望，也就是这组数据的平均数；这里的σ指的就是标准差，标准差就是方差开根号。$σ^2$就是方差，所以它描述的是这组数据的分散程度。

正态分布的性质

  1. 曲线在x轴上方，与x轴不相交；
  2. 曲线是单峰的，它关于直线x=μ对称；
  3. 曲线在x=μ处达到顶峰$$1\over \sqrt{2\pi}σ$$；
  4. 曲线与x围成的面积是1；
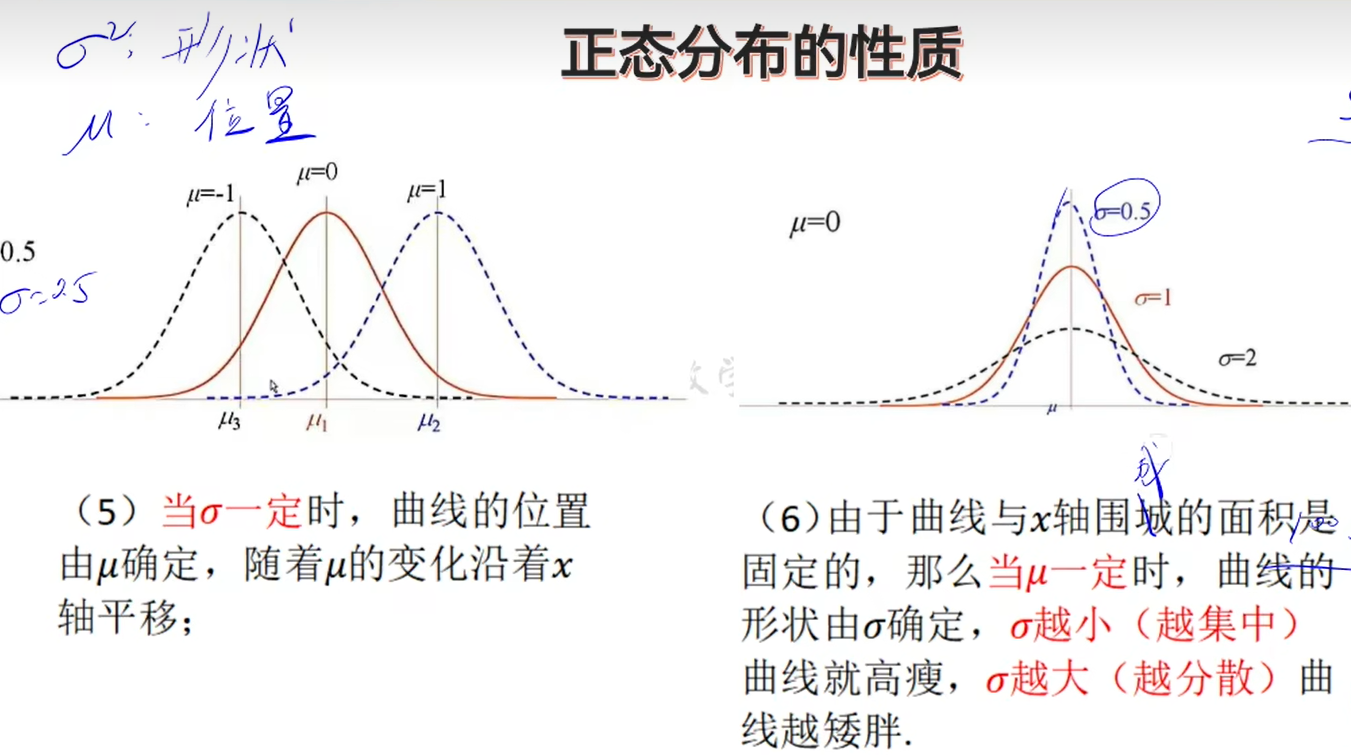
  5. 当σ一定时，曲线的位置由μ确定，随着μ的变化沿着x轴平移；
  6. 由于曲线与x轴围成的面积是固定的（是1），那么当μ一定时，曲线的形状由σ确定，σ越小（越集中）曲线就高瘦，σ越大（越分散）曲线越矮胖。

image-20230408172527840

3σ原则

image-20230408173113806

image-20230409000546681

视频地址：十分钟理解正态分布及其应用

美国高考分为SAT和ACT，学生可以自主选择两个中的一个。SAT的满分是1600分，ACT的满分是36。

现在美国一所大学收到了两名同学Ann和Tom的申请，Ann提交的是SAT成绩：1300，Tom提交的是ACT成绩：24

当年SAT的均值是1100，标准差是200；当年ACT的均值是21，标准差是6。

现在美国大学的招生官要考虑：Ann和Tom谁的高考成绩更优秀呢？

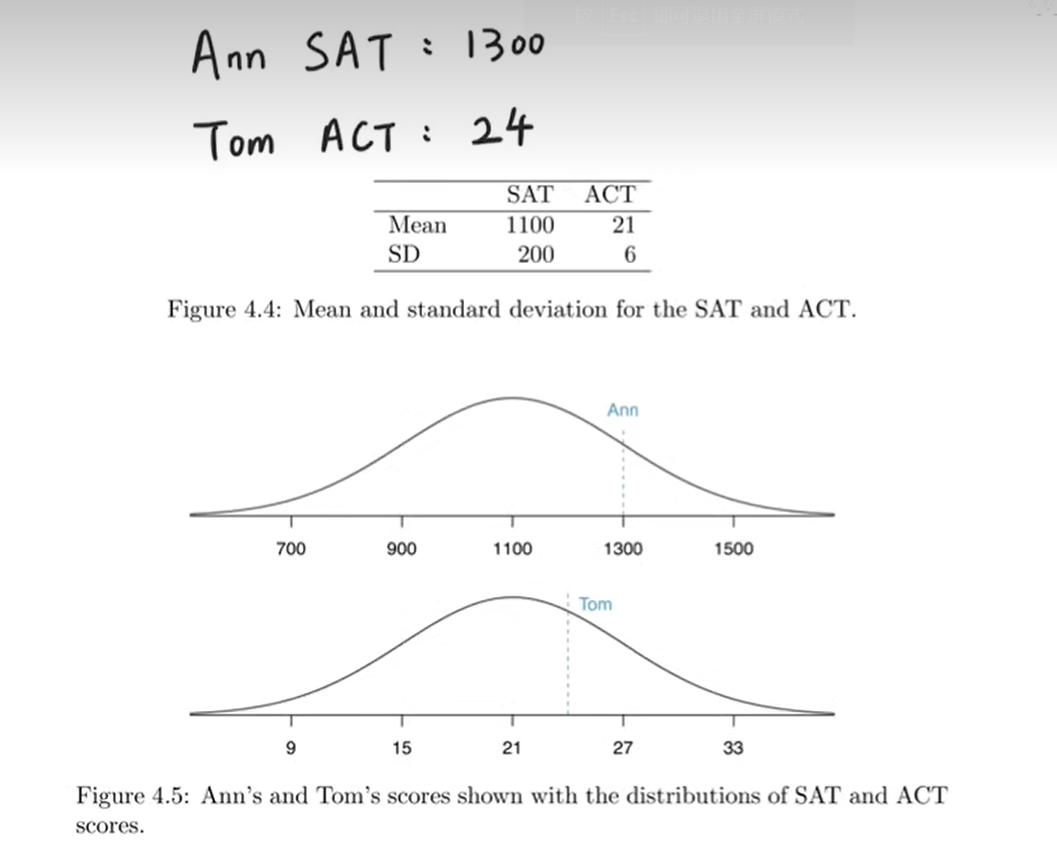
image-20230408174636916

通过直觉感受到，谁的成绩距离均值越远，说明他越优秀。

但这里的问题是，SAT和ACT使用的是不同的分数制，即数据尺度不同。我们应该怎样衡量距离均值的远近呢？

标准差σ具有的含义就是：数据离均值的平均距离。

Ann：$$1300-1100\over 200$$=1

Tom:$$24-21\over 6$$=0.5

Ann超过了均值200分，这200分是几个标准差呢？除以标准差200后得知，是1个标准差。

Tom超过了均值3分，这3分是几个标准差呢？除以标准差6后得知，是0.5个标准差。

这说明Ann比Tom更优秀。

现在我们把这个思想一般化一下。就是z分数（z-score）。

跳转锚点1

上面提到过的z分数
$$
z={x-μ\over σ}
$$
它的含义就是——数据距离均值有几个标准差。

E(z)=0，SD(z)=1。

z服从标准正态分布，即Z~N(0,1)。

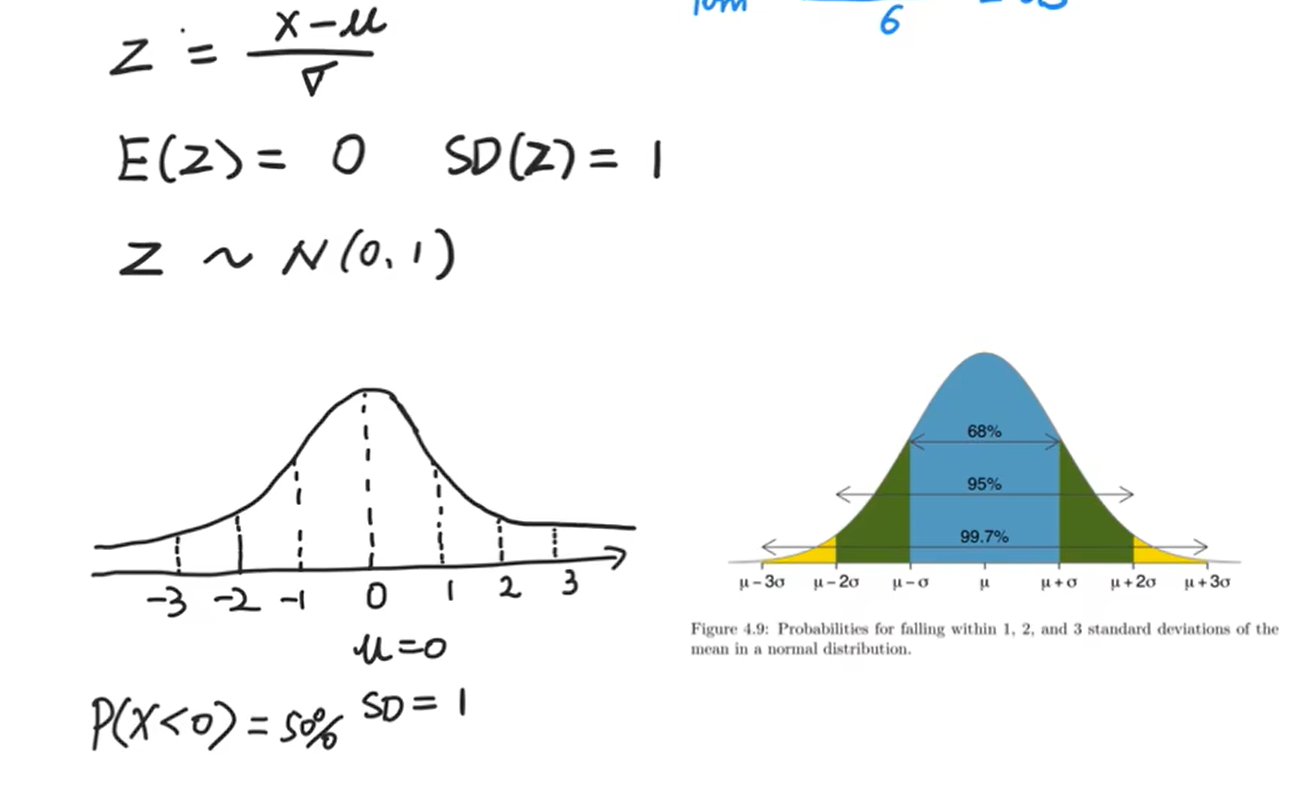
image-20230408181636147

我们上面提到过的正态分布的经验法则同样适用于标准正态分布。

P(Z<0)=50%

P(-1<z<1)=68%

P(-2<z<2)=95%

我们回到刚才Ann和Tom的例子。

Ann的SAT成绩是1300分，那么Ann在所有SAT的考生中是前百分之几呢？

之前我们已经计算过了，Ann的z-score=1

即图中阴影部分的百分比是多少。

image-20230408182428194

根据对称性和经验法则，有：

image-20230408182557664

即Ann是全体考生中的前16%，超过了1-16%=84%的SAT考生。

那么Tom呢？

Tom的z分数是0.50。我们通过查表（先在竖列查小数点后第一位对应的行，再在横行查小数点后第二位对应的列）最终确定P(z<0.50)=0.6915。即Tom超过了ACT考生中的69.15%。

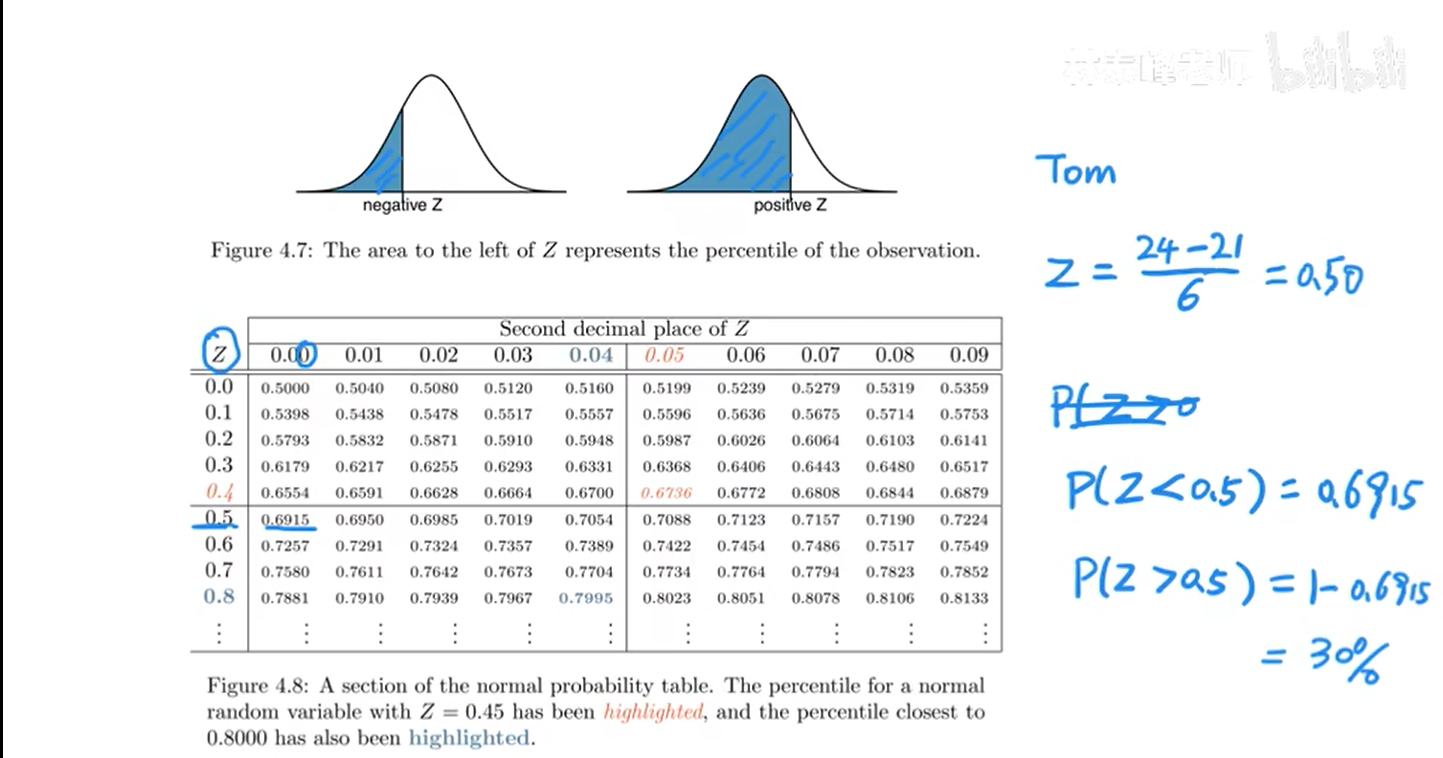
image-20230408182838011

Tom是ACT考生中的前P(z>0.50)=1-0.6915≈30%。