第6章 高等概率论

[toc]

6.1 互补事件

对于包含两个事件以上的事件集，如果事件集中至少有一个事件发生，我们称这些事件为互补事件。比如：

  • 对于事件集{温度低于60℃，温度高于90℃}，这些事件不是互补事件，因为温度有可能介于60℃和90℃之间。事实上，这两个事件是互斥事件（mutually exhaustive），因为温度不可能同时低于60℃、高于90℃。
  • 掷骰子事件集{1，2，3，4，5，6}是互补事件，因为这些事件是所有骰子可能出现的点数骰子点数肯定是其中之一。

6.2 重温贝叶斯思想

简单来说，当我们讨论贝叶斯时，我们关注以下3个事情和它们之间的关系：

  • 先验分布（prior distribution）
  • 后验分布（posterior distribution）
  • 似然度（likelihood）

通常来讲，我们更关心后验分布，因为它是我们想知道的答案。

另一种理解贝叶斯思想的方法是，数据会影响我们的判断。我们有一个先验概率，或者有一个关于假设朴素的想法，然后根据历史数据，得出该假设的后验概率。

6.2.1 贝叶斯定理

贝叶斯定理是贝叶斯推理的重要结果。下面我们将介绍它的推导过程。回忆我们之前介绍过的定义：

  • P(A)=事件A发生的概率。
  • P(A|B)=事件B发生的前提下，事件A发生的概率。
  • P(A,B)=P(A $\cap$ B)=事件A和事件B同时发生的概率。
  • P(A,B)=P(A $\cap$ B)=P(A)×P(B|A)。

最后一个公式指，事件A和事件B同时发生的概率，等于事件A发生的概率乘以事件A发生的前提下事件B发生的概率。这个公式就是贝叶斯定理的由来。

已知：
$$
P(A,B)=P(A)·P(B|A)
\
P(B,A)=P(B)·P(A|B)
\
P(A,B)=P(B,A)
$$
因此：
$$
P(B)·P(A|B)=P(A)·P(B|A)
$$
两边同时除以P(B)后即得到贝叶斯定理，如下所示：
$$
P(A|B)={P(A)×P(B|A)\over P(B)}
$$
我们还可以尝试从假设（hypothesis）和数据（data）的角度看待贝叶斯定理。如果用D表示收集的数据，H表示你的初始假设，贝叶斯定理可以被理解为求解P(H|D)，即在给定数据D的前提下，初始假设成立的概率，用公式表示为：
$$
P(H|D)={P(D|H)P(H)\over P(D)}
$$

我们有一个初始假设H，收集数据（Data）或证据（Evidence）后，更新（update）我们的看法，即P(H|D)

其中：

  • P(H)指在收集数据前，假设发生的概率，称为先验概率；
  • P(H|D)是待求解的概率，指在收集数据后，假设发生的概率，称为后验概率；
  • P(D|H)是给定假设下，数据发生的概率，称为似然度；
  • P(D)指在任何假设下，数据发生的概率，称为标准化常量。

这一思想已经离机器学习和预测分析不远了。在很多案例中，当我们做预测分析时，指的正是根据已有数据预测未来。用术语表示，假设H是待预测的结果，P(H|D)可以理解为：在给定数据的前提下，假设H发生的概率是多少？

下面我们通过一个例子演示贝叶斯定理如何在工作场合中发挥作用。

假设有Lucy和Avinash两名员工同时为公司撰写博客。根据历史数据，你对Lucy 80%的文章非常满意，但只对Avinash 50%的文章表示满意。某天上午，一篇没有署名的新文章放在你的办公桌前。你非常喜欢这篇文章，给其评价A+。假设这两位作者发布文章的频率一致，请问这篇文章来自Avinash的概率是多少？

在你彻底崩溃之前，让我们先像经验丰富的数学家那样，列出所有的已知信息。

  • 假设H：这篇文章的作者是Avinash；
  • 数据D：你喜欢这篇文章；
  • P(H|D)：在已知你喜欢文章的前提下，作者是Avinash的概率；
  • P(D|H)：在作者是Avinash的前提下，你喜欢该文章的概率；
  • P(H)：这篇文章作者是Avinash的概率；
  • P(D)：你喜欢这篇文章的概率。

请注意，如果缺失上下文，以上某些变量可能没有任何意义。比如P(D)，它可以是你喜欢每一篇出现在办公室上的文章。这听起来非常诡异，但请相信我，在贝叶斯定理中，它是有意义的。同样地，P(D)并不依赖文章的来源，而是指对于任何来源的文章，你喜欢的概率。

下面，我们尝试用贝叶斯定理计算P(H|D)。
$$
P(H|D)={P(D|H)P(H)\over P(D)}
$$
等等！我们有公式右边的值吗？当然有！如下所示。

  • P(H)是该文章来自Avinash的概率。由于两位作者发布博客的频率相等，我们可以认为该文章有一半的概率来自Avinash。
  • P(D|H)是你喜欢Avinash文章的比例，我们已知是50%。
  • P(D)比较有意思。它指通常情况下，你喜欢一篇文章的概率。这意味着我们需要考虑文章来自Lucy等其他作者的情况。如果所有的假设能够组成一个套件（suite），我们就可以使用上一章介绍的概率法则。我们将由完全互斥且互不相交的假设组成的集合称为套件。简单来说，对于套件中的假设，有且仅有一个假设发生。在本例中，两个假设分别是“文章来自Lucy”和“文章来自Avinash”。显然，这两个假设可以构成套件，因为：文章至少来自其中一人；文章最多来自其中一人；因此，只有一人是文章的作者。

当我们有了套件，就可以使用乘法和加法法则，如下所示。
$$
D=(文章来自Avinash且你喜欢它)或(文章来自Lucy且你喜欢它)
\
P(D)=P(你喜欢它且文章来自Avinash)或P(你喜欢它且文章来自Lucy)
\
P(D)=P(文章来自Avinash)×P(你喜欢它|文章来自Avinash)+P(文章来自Lucy)×P(你喜欢它|文章来自Lucy)
\
P(D)=0.5×(0.5)+0.5×(0.8)=0.65
$$
不错，继续努力！下面可以完成我们的等式：
$$
P(H|D)={P(D|H)P(H)\over P(D)}
\
P(H|D)={0.5×0.5\over 0.65}=0.38
$$
因此，这篇文章来自Avinash的概率是0.38。P(H)=0.5和P(H|D)=0.38有点意思。P(H)=0.5指在没有任何数据的前提下，文章来自Avinash的概率是50%，和抛硬币得到正面或反面的概率一样。如果给定了数据（你是否喜欢该博客），假设发生的概率发生了变化，低于0.5。这正是贝叶斯思想的本质——根据先验假设和给定的数据，更新对事件的后验假设概率。

3Blue1Brown：证据（Evidence）并不应直接决定你的看法，而是更新（update）看法。

3Blue1Brown的视频

3Blue1Brown的视频将有助于我们理解贝叶斯定理。

视频地址：【官方双语 贝叶斯定理，使概率论直觉化】

在看公式和推理之前，我们先来看看Steve的故事：

image-20230323112507759

Steve是个图书管理员的概率更大还是Steve是个农民的概率更大呢？

根据实验结果，当人们知道Steve是“一个温顺又井井有条的人”后，大多数人都会说他更有可能是图书管理员。

关键在于，在做判断的时候，没人把农民和图书管理员的比例信息考虑进去。

在美国，农民与图书管理员的数量之比是20:1。

我们假设一个样本，这个样本中有10名图书管理员和200名农民。

我们假设40%的图书管理员符合”温顺又井井有条“，而农民中符合条件的只有10%。那么就是说，在这个样本中，有4名图书管理员和20名农民符合条件。
$$
P(\textcolor{red}{Librarian}\quad given\quad \textcolor{blue}{description})
$$
所以即使你认为符合这个描述的人是一个图书管理员的可能性是是一个农民的4倍，也抵不过农民的数量很多。

image-20230324152358213

你有一些假设（Hypothesis），比如“Steve是一个图书管理员”。

同时你得到了一些证据（Evidence），或者称为数据（Data），比如口头描述“Steve是一个温顺而又井井有条的人”。

证据或者说数据可能是你用各种方法收集到的，比如找到了数据集、用爬虫爬取等等。

3B1B的视频中称为证据，本书中称为数据。

并且你想知道，在“你得到的证据是真的”的条件下，你的假设成立的概率。

即：
$$
P(\textcolor{red}{Hypothesis}\quad given\quad \textcolor{blue}{the\quad evidence})
$$
用符号表示为P(H|E)。

也就是说，我们把我们考虑的情况限制在了证据正确的可能性（条件）下。

P(H)是在考虑新证据之前，假设成立的可能性。在我们的例子中，P(H)指Steve是一个图书管理员的概率，即1/21。这个数字来自人群中图书管理员和农民的比例。

这个数字P(H)叫作先验概率（prior）。

之后我们要考虑，图书管理员中符合这个描述的比例——在假设成立的情况下我们看到证据的概率。即P(E|H)。

3B1B：当你看到这个竖杠，就表明我们只在讨论总概率空间中的一个有限的部分。

在这个例子中，有限的部分就是左侧那一块，即假设成立（是图书管理员）的条件下，符合证据E的概率。

image-20230324154624057

P(E|H)被称为似然概率（likelihood）。

类似的，你需要知道概率空间的另一侧包含多少证据——在假设不成立的情况下我们看到证据的概率，即P(E|┐H)。

在本例中，P(E|H)=0.4，P(E|┐H)=0.1。

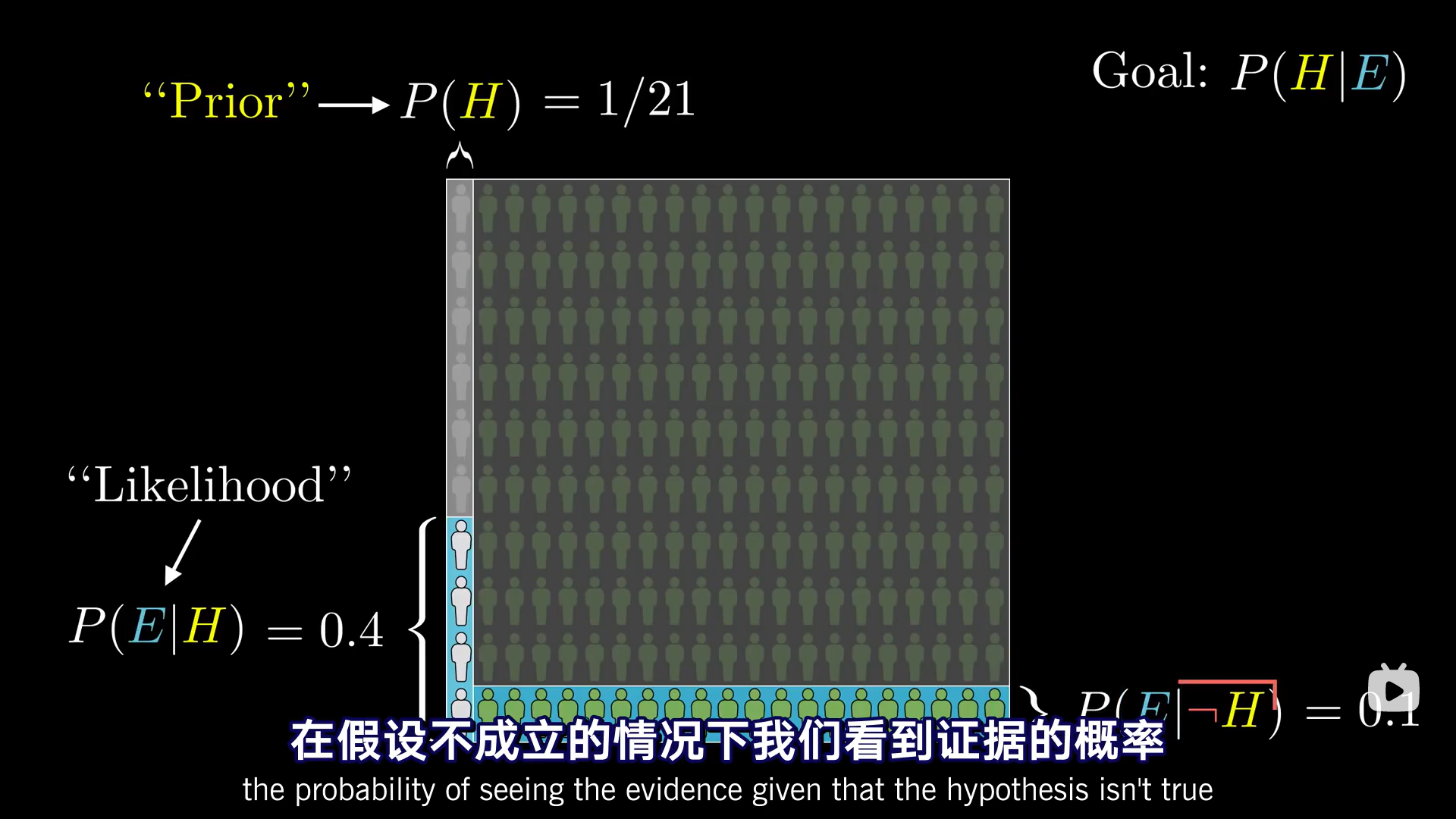
image-20230324155403927

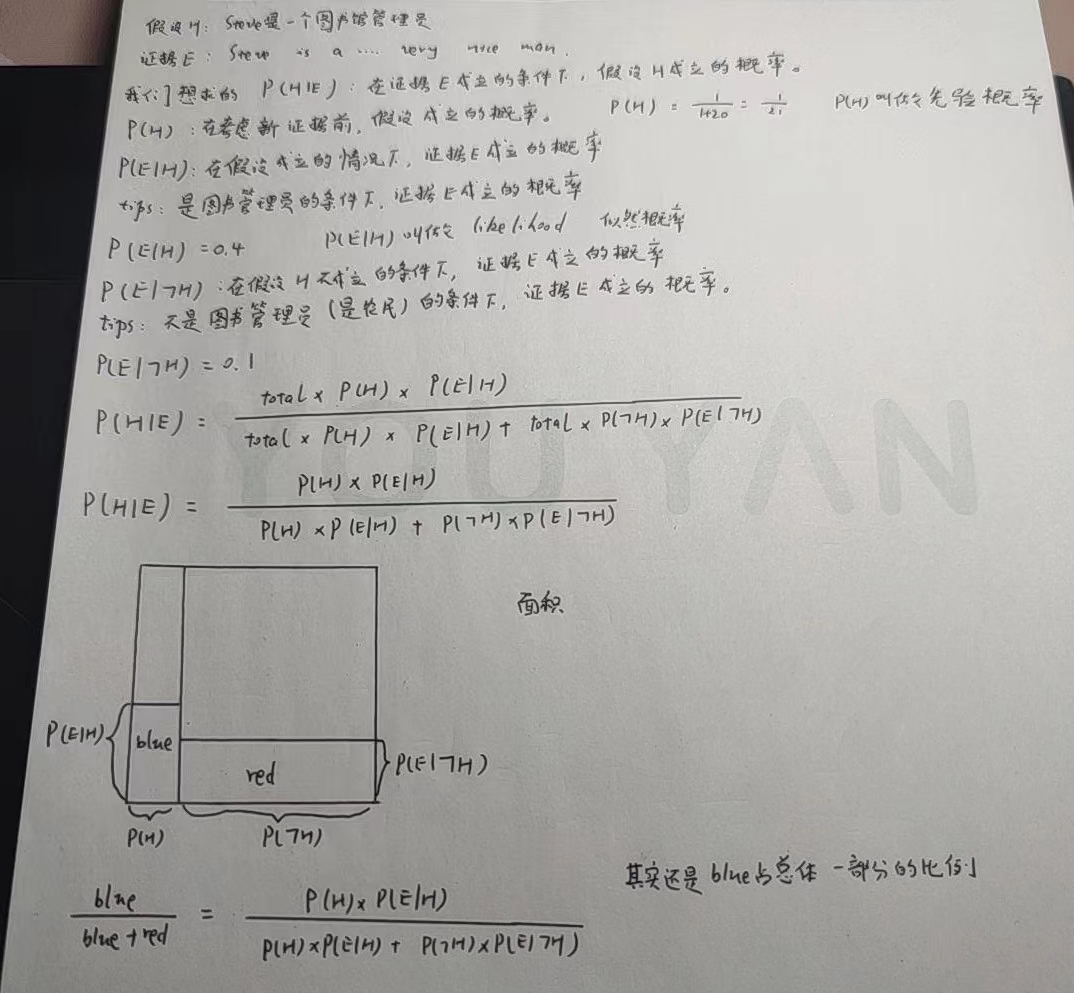
我们想求的P(H|E)，即在证据为真的条件下是图书管理员假设成立的概率：
$$
P(\textcolor{red}H|\textcolor{blue}E)={total·P(\textcolor{red}H)·P(\textcolor{blue}E|\textcolor{red}H)\over total·P(\textcolor{red}H)·P(\textcolor{blue}E|\textcolor{red}H)+total·P(┐\textcolor{red}H)·P(\textcolor{blue}E|┐\textcolor{red}H)}
$$

total指总人数，210人。

total×P(H)得到的是图书管理员的数量，即总共有10个图书管理员。

total×P(H)×P(E|H)，即图书管理员的数量×P(E|H)，指在概率空间/样本空间为图书管理员的条件下，E发生的概率（符合证据的概率）。

total×P(┐H)，得到的是不是图书管理员，即农民的数量。

total×P(┐H)×P(E|┐H)，指在概率空间不是图书管理员的条件下，E成立的概率。

其实，这个过程在一步一步地限制概率空间/样本空间。以total×P(H)×P(E|H)为例，一开始的概率空间为总体，乘上P(H)后，概率空间由总体（图书管理员+农民）变为图书管理员，再乘上P(E|H)，指的是，在概率空间为图书管理员的条件下，符合证据E的概率。

total可以被约分掉。

最终得到的结果即：
$$
P(\textcolor{red}H|\textcolor{blue}E)={P(\textcolor{red}H)·P(\textcolor{blue}E|\textcolor{red}H)\over P(\textcolor{red}H)·P(\textcolor{blue}E|\textcolor{red}H)+P(┐\textcolor{red}H)·P(\textcolor{blue}E|┐\textcolor{red}H)}
$$
这就是贝叶斯定理（Bayes’s theorem）。

多数情况下，你会看到分母简写成P(E)，实际上，你如果要算P(E)，你还是需要把它拆分成假设成立和假设不成立两部分来计算。

最终计算出的结果P(H|E)叫作后验概率（posterior）。也就是你看到证据后，你对假设成立与否的看法。

image-20230324172146456

我们把整个概率空间想象成一个1×1的正方形，之后，任何事件都对应概率空间的一个子集，并且事件发生的概率就是子集的面积。

从几何的角度去考虑，P(H)×P(E|H)，也就是左边矩形的宽度乘以高度，即左边矩形的面积。

现在试着考虑一个更大的问题：如何让概率更直观。

Kahneman和Tversky做了另一个实验（Steve的问题就是他们做的一个实验）。

当人们听到描述后，被问到以下哪个选项可能性更大：

image-20230324172953460

85%的实验者说后者更有可能！

但是实际上，选项2是选项1的子集！

更有趣的是，只要我们对这个问题简单地组织一下语言，错误率就能从85% 讲到0。

image-20230324173146090

下面是对直觉（直观感受）的准确度排名：

100个当中有40个＞40%＞0.4＞“What’s more likely …?”

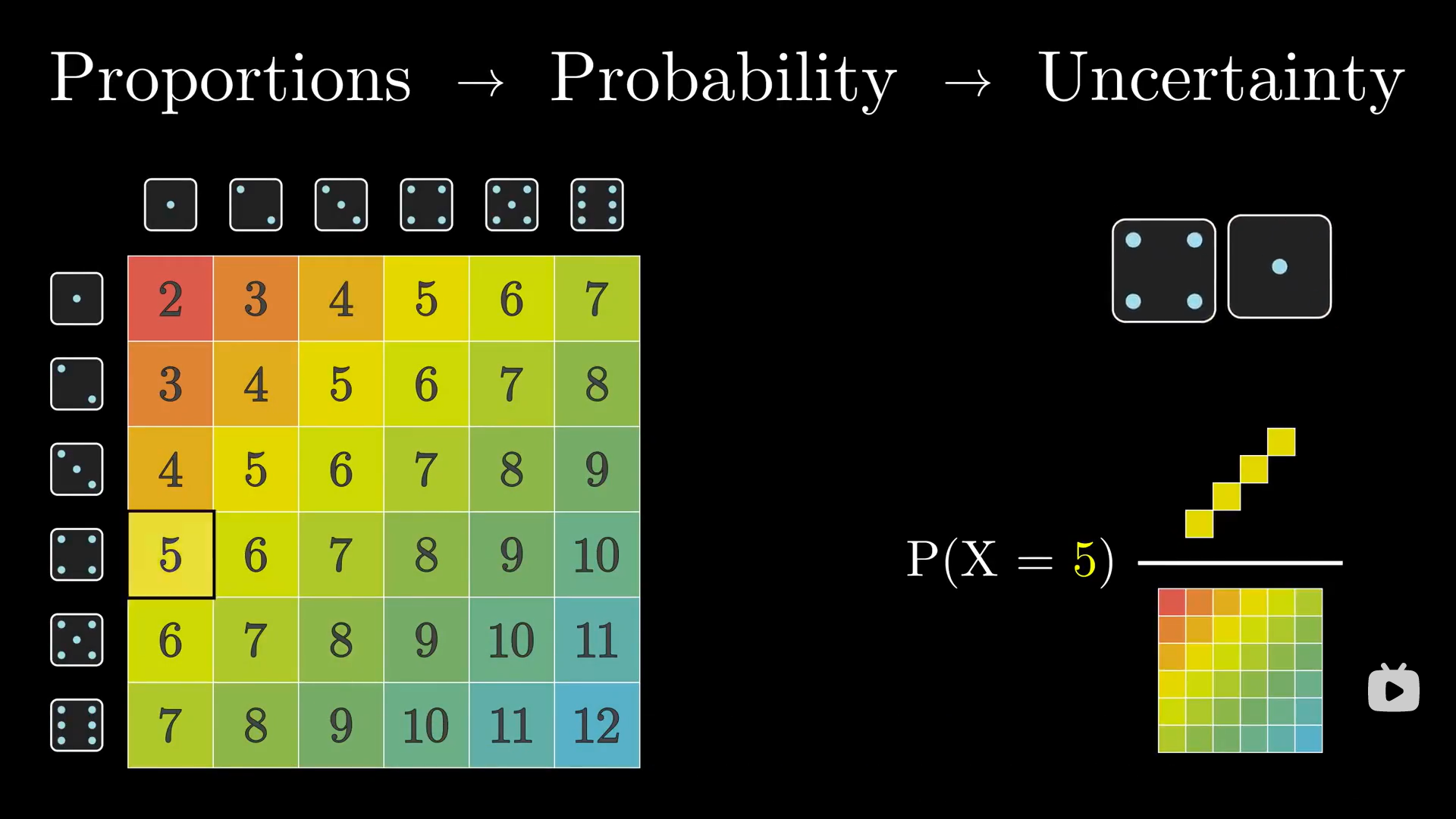
3Blue1Brown：人们认为概率论就是研究“不确定”，确实，概率论就是这样应用在科学上的。但是概率的数学本质确实就是数学上所说的比例，这些公式也都是由数学比例构成的。

image-20230324173536483

382e46ac247c106d22aebf9591f112e

一道习题

问题：假设人群中肺炎的感染率为0.1%，肺炎检测的正确率为99%，一个人肺炎检测结果为阳性，求他患有肺炎的概率。

4c0cb8da49331c5bb2fe7d6755ba08d

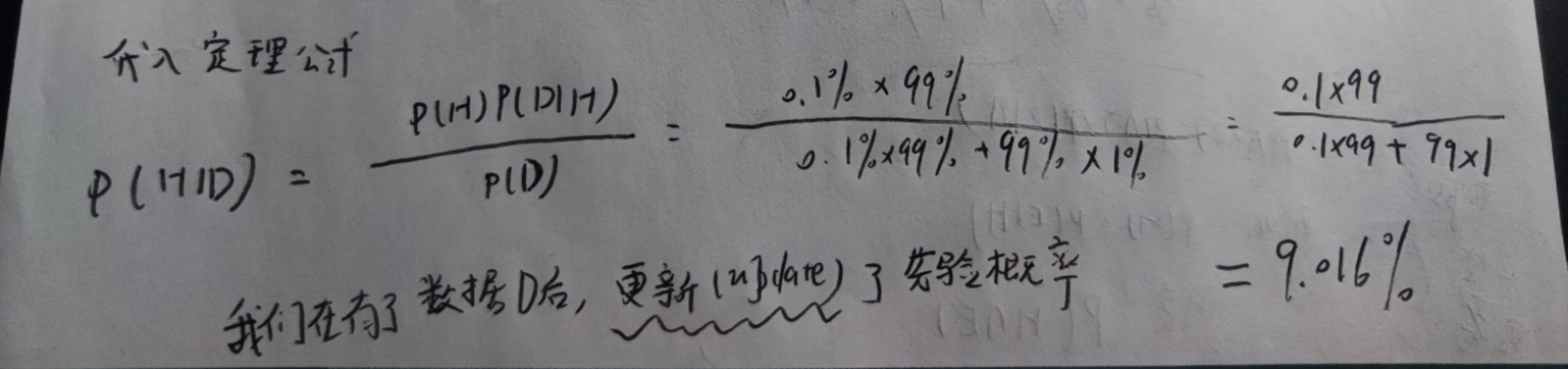
66214fcddaa30284a4fdee9db0bdb0e

寻找黄金船

3Blue1Brown在视频里提到，在20世纪80年代，由Tommy Thompson带领的一支队伍利用贝叶斯搜寻策略，协助他们发现了一艘一个半世纪前的沉船，以今天的价格计算，这艘船装了价值7亿美元的黄金！

视频地址：【假装讲课】找丢失的船时如何省力

背景故事：

有一艘船载满了黄金，有一天该船按照既定航线航行时，突然失去了联络。我们应该如何派出搜救队/打捞队？

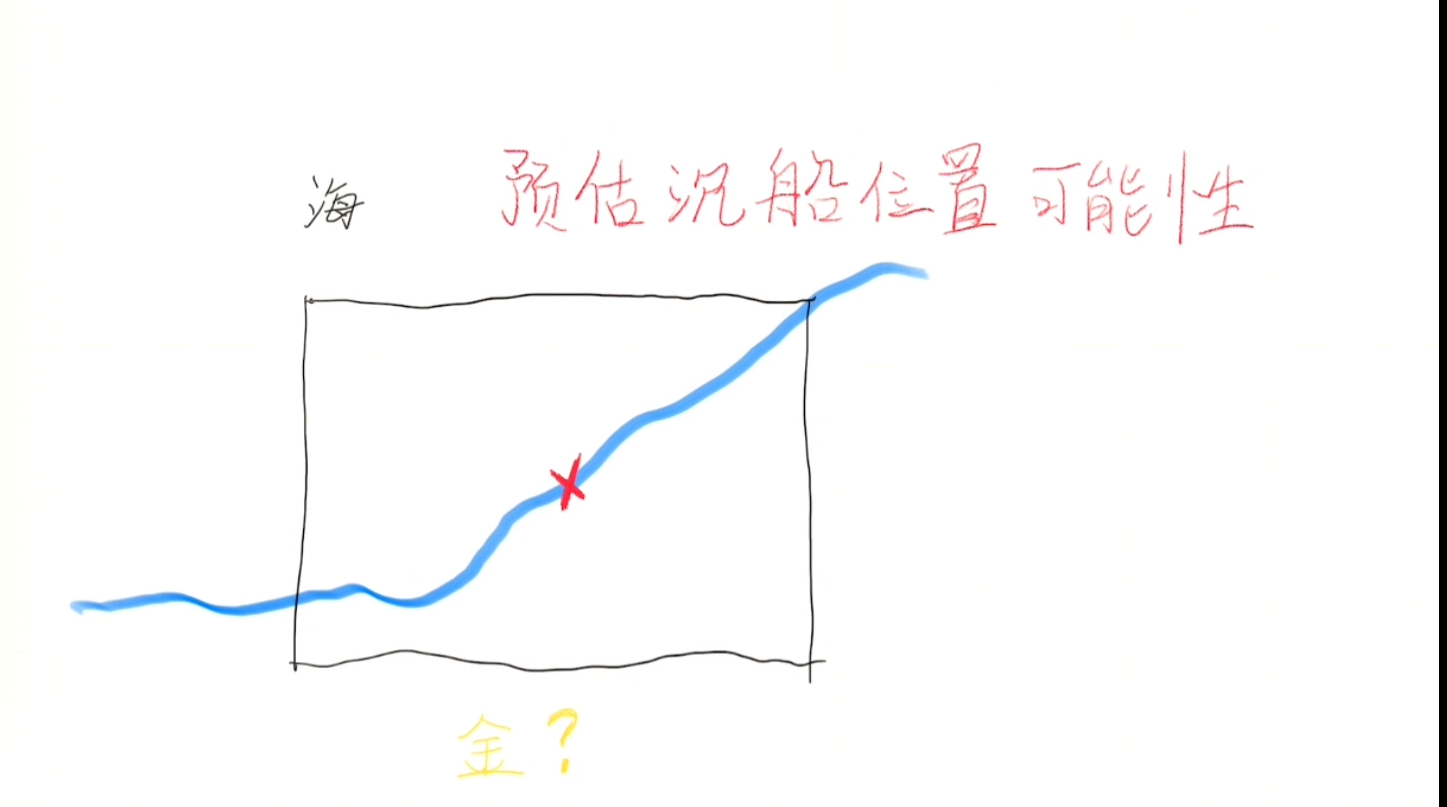
image-20230324201502394

预估沉船位置可能性

专业人士可能会考虑洋流、船长开船习惯、风向等因素，来做出一个推测。

我们可以把推测出的位置（位置范围）标在地图上面。

即，我们有了P(船在这里)

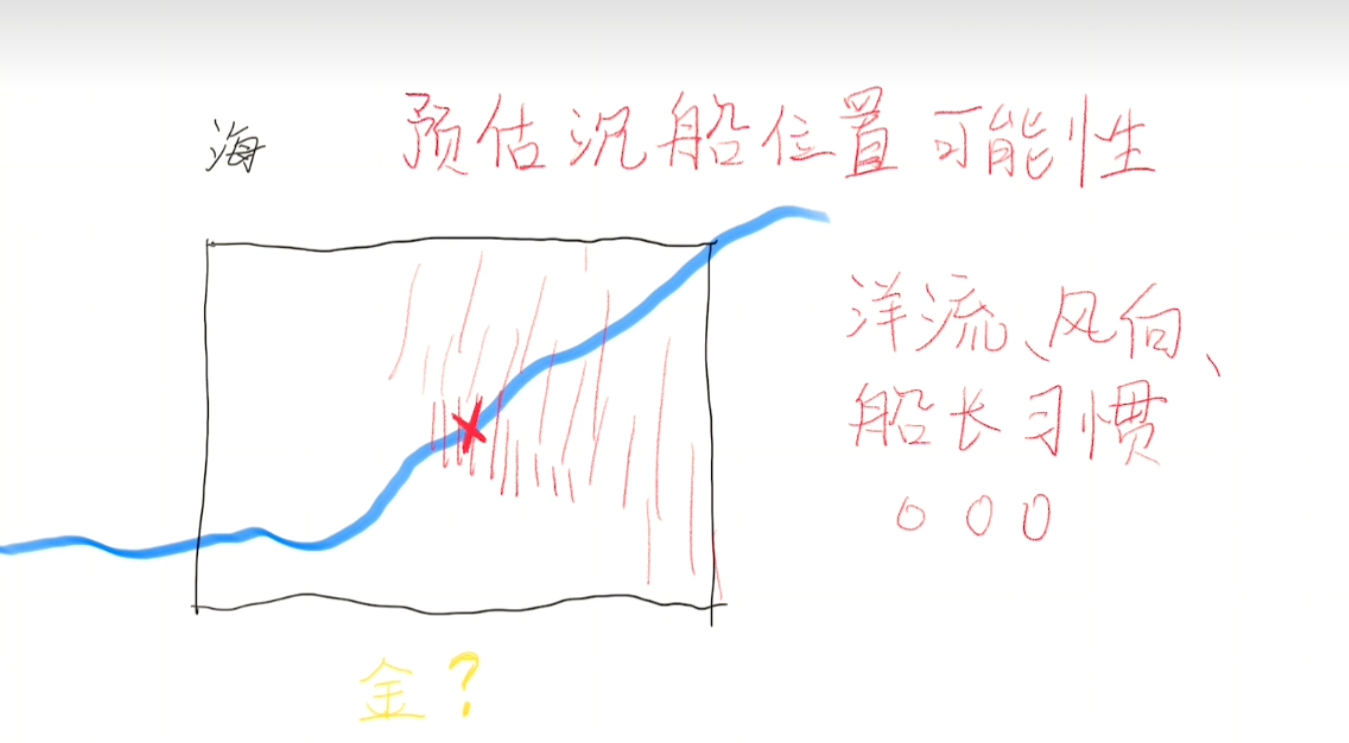
image-20230324201833825

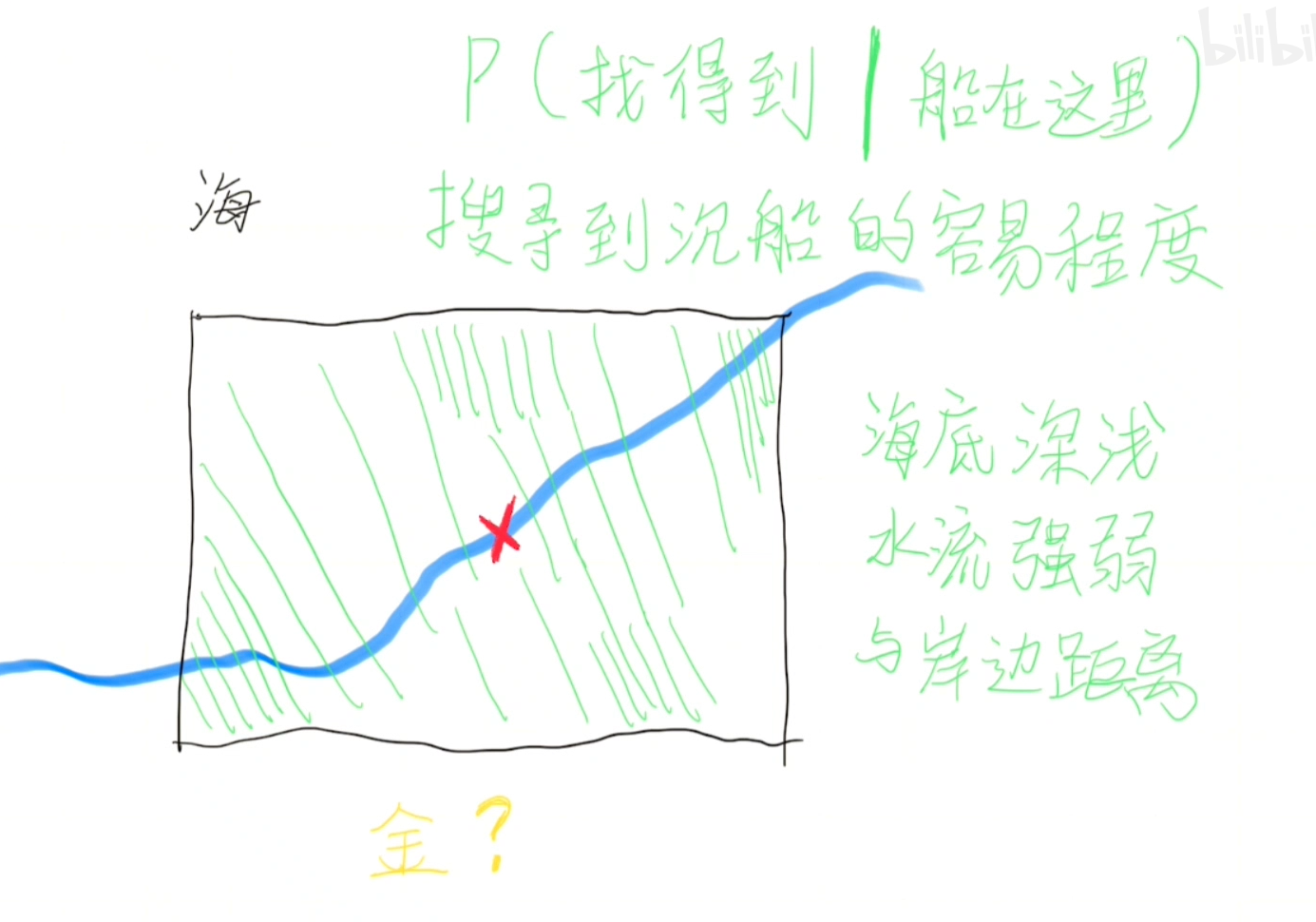
搜寻到沉船的容易程度

这个船即使就在搜寻的位置，也有可能受海底深浅、水流强弱、与岸边距离等因素影响而无法找到。

用公式表达为：
$$
P(找得到|船在这里)
$$
然后我们一样将它画在地图上。

image-20230324202209127

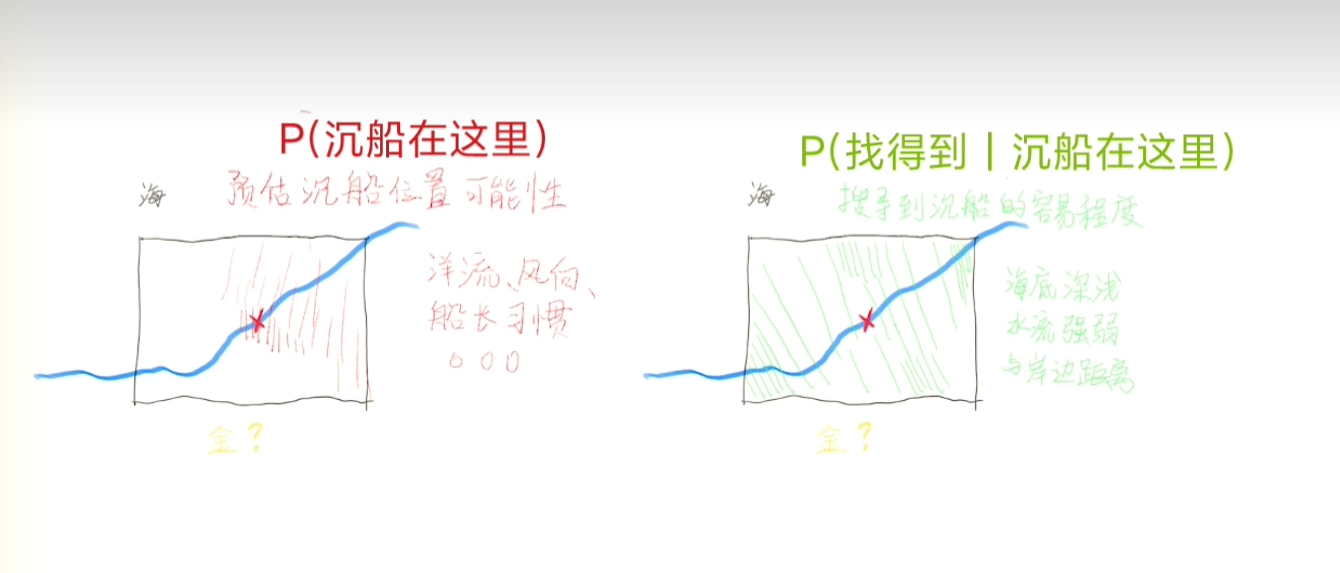
image-20230324202322583

根据条件概率公式，我们将上面两个内容乘一下。
$$
P(找得到船)=P(沉船在这里)×P(找得到|沉船在这里)
$$
我们从P(找得到船)最大的地方开始找。

我们把刚才两个概率相乘的结果标在地图上，然后挑选概率最大的那个点开始寻找。

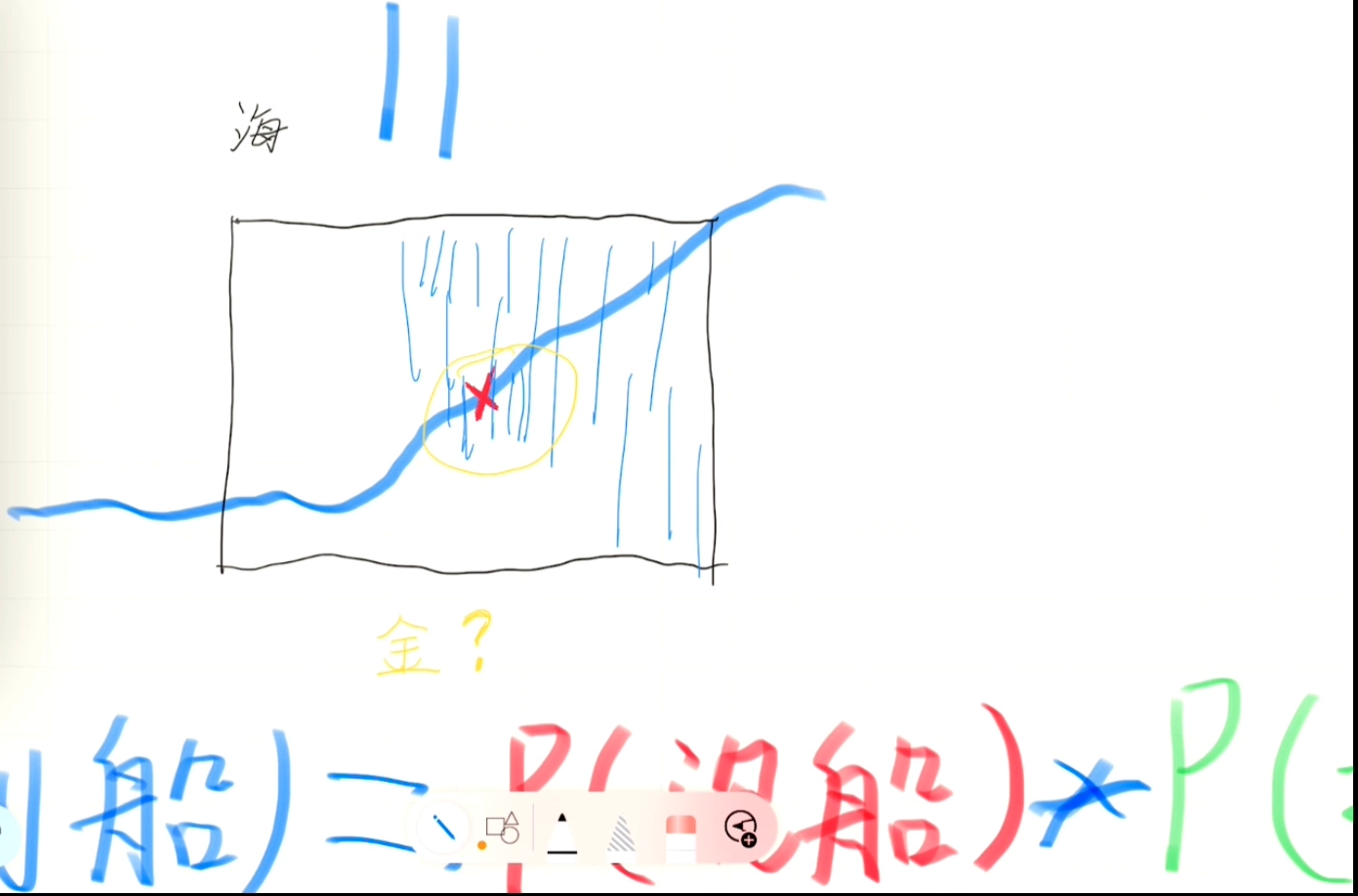
image-20230324202927399

我们如果找到了，就可以直接宣布成功。如果没找到，就更新一下找得到船的概率地图，再从更新后概率最高的地方继续寻找。

为什么一定要更新概率地图呢？不可以接着从概率第二高的地方找下去吗？

这里的问题在于，我们即使找过了第一个地方并且没找到，船也仍然有可能在第一个地方，只不过我们没找到而已。

所以我们需要确定第一个地方到底值不值得我们继续寻找。
也就是计算一下，我们没找到的条件下，船在这里的概率。

那么根据贝叶斯定理：
$$
P(沉船在这里|没找到)={P(没找到|沉船在这里)·P(沉船在这里)\over P(没找到)}={P(没找到|沉船在这里)·P(沉船在这里)\over P(没找到&沉船在这里)+P(没找到&沉船不在这里)}
$$
091f23f86b00e0f991ae875ca822549

我们在黄圈内没找到船但是船还在那里的概率已经用已知量表示出来了。

我们现在需要把更新后的概率更新到原来的概率地图上，然后再找到概率最高的点作为下一次找船的地点。

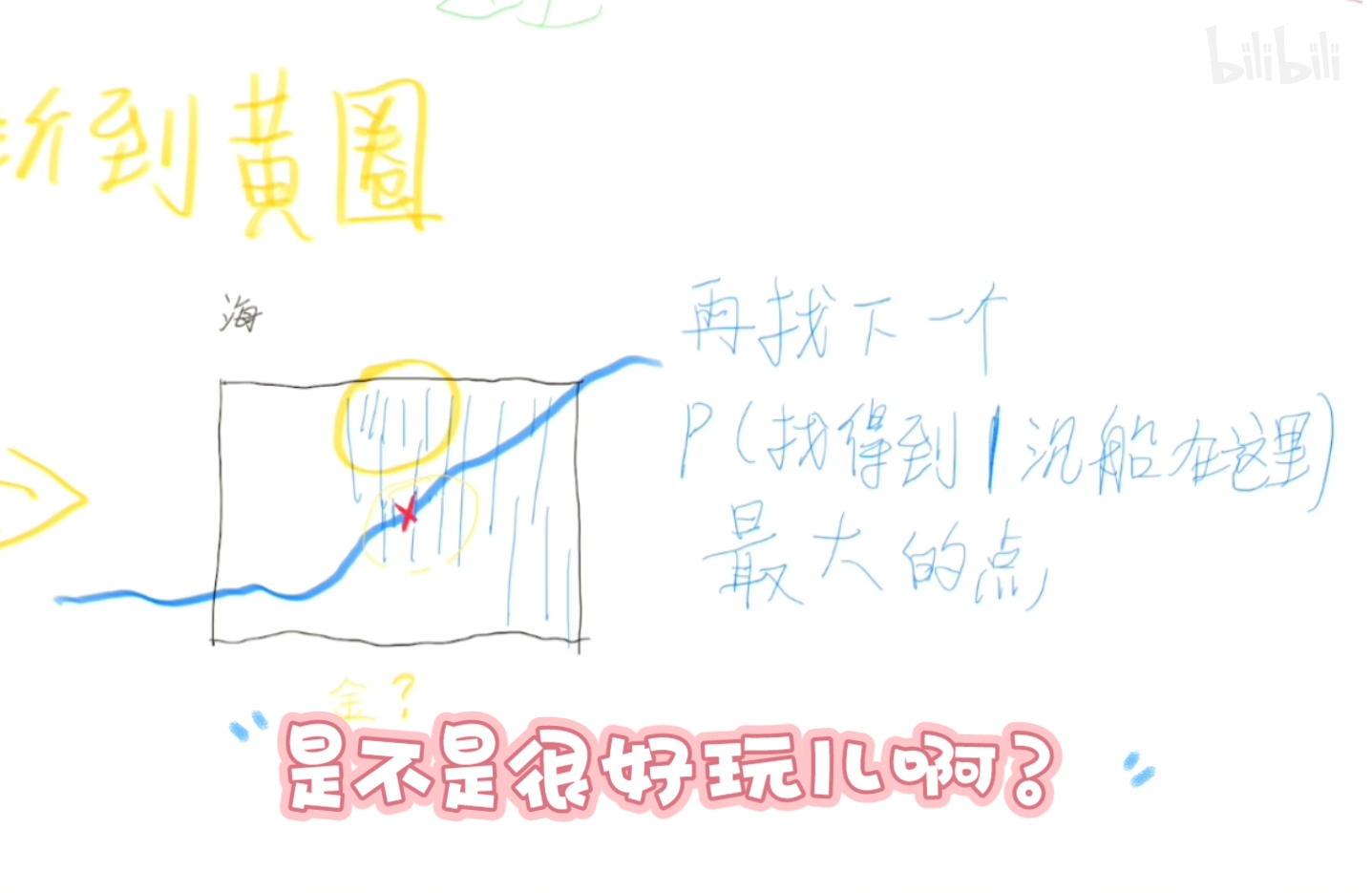
image-20230324213229873

6.2.2 贝叶斯定理的更多应用

通常情况下，当我们需要依据数据和概率快速做出决策时，贝叶斯定理就能派上用场。大部分推荐引擎，比如Netflix，都或多或少地使用了贝叶斯定理。我们很容易就能想通其中的道理。

在简化的场景中，假设Netflix只有10种类型影片可供选择。如果没有任何用户数据，用户喜欢喜剧类型影片的概率是1/10。

当用户给喜剧电影5星评价后（满分5星），请问Netflix猜测用户喜欢另一部喜剧电影的概率是多少？显然这个概率将比随机猜测概率10%高。

下面我们将在更多数据和案例中应用贝叶斯定理。

案例：泰坦尼克

一个有名的案例是研究1912年沉没的泰坦尼克号数据。我们将使用概率论方法，研究乘客生还情况是否具有人口统计学特征。换句话说，我们想从数据集中抽离出核心特征，寻找哪种类型的乘客将在此次灾难中生还。

首先，我们加载泰坦尼克号数据。

1
2
3
4
import pandas as pd
titanic=pd.read_csv('data/titanic.csv')  #read in a csv
titanic=titanic[['Sex','Survived']]      #the Sex and Survived column
titanic.head()
Sex Survived
0 male no
1 female yes
2 female yes
3 female yes
4 male no

在表格中，每行代表一名乘客。我们提取了两个重要特征：性别（Sex）和是否幸存（Survived）。第1行表示一名没有幸存的男性乘客，第4行（Python索引为3）表示一名幸存的女性乘客。

我们先从简单的概率入手。首先计算在不考虑性别的情况下，每名乘客的生还概率。方法是计算Survived列值为yes的行数，再除以总行数。

1
2
3
num_rows=float(titanic.shape[0])    #==891 rows
p_survived=(titanic.Survived=="yes").sum()/num_rows  #==.38
p_notsurvived=1-p_survived                           #==.61

请注意，我们已经有P(Survived)，可以根据互斥法则计算P(Died)。下面，我们分别计算男性和女性的生还率：

1
2
p_male=(titanic.Sex=="male").sum()/num_rows  #==.65
p_female=1-p_male                            #==.35

现在，请问自己一个问题：性别是否是影响生还率的重要特征？为了回答这个问题，我们需要计算P(Survived|Female)，即已知乘客为女性的情况下的生还率。为此，我们将生还的女性乘客数量除以女性乘客总数，公式如下：
$$
P(生还|女性)={P(女性且生还)\over P(女性)}
$$

1
2
3
4
number_of_women=titanic[titanic.Sex=='female'].shape[0]  #==314
women_who_lived=titanic[(titanic.Sex=='female')&(titanic.Survived=='yes')].shape[0] #==233
p_survived_given_woman=women_who_lived / float(number_of_women)
p_survived_given_women  #==.74

女性的生还率0.74远大于全体的生还率0.38！这说明性别是影响生还的重要特征。

案例：医疗案例

贝叶斯定理的经典用途之一是医学实验分析。在学校和工作场所，对违禁药物的检查已经越来越普遍。检测公司认为自己的检查方法非常灵敏，（基本上）只要使用了违禁药物，检测结果都会呈阳性。同时，他们声称检测也具有较高特异性，如果未使用违禁药物，检测结果将呈阴性。

假设平均来看，药物检测的敏感性为60%，特异性为99%。也就是说，如果雇员使用了违禁药物，检测结果有60%的概率呈阳性；如果雇员未使用违禁药物，检测结果有99%的概率呈阴性。

假设我们在违禁药物使用率为5%的工作场所进行检测，我们想知道如果检测结果是阳性，那么雇员使用违禁药物的概率是多少？

按照贝叶斯定理，我们需要计算使用了违禁药物且检测结果为阳性的概率：

  • 用D表示使用了违禁药物；
  • 用E表示检测结果为阳性；
  • 用N表示未使用违禁药物。
  • 待求解的对象是P(D|E)。

根据贝叶斯定理：
$$
P(D|E)={P(E|D)P(D)\over P(E)}
$$
先验概率P(D)是在检测之前，雇员使用违禁药物的概率5%。似然度P(E|D)是使用了违禁药品且检测结果为阳性的概率，即检测的敏感性60%。常数P(E)则比较特殊。我们需要考虑两种可能性：P(E且D)和P(E且N)，即还要考虑到雇员未使用违禁药物，但检测结果为阳性的错误检测情况。
$$
P(E)=P(E且D)+P(E且N)
\
P(E)=P(D)P(E|D)+P(N)P(E|N)
\
P(E)=0.05×0.6+0.95×0.01
\
P(E)=0.0395
$$
因此，之前的公式变为：
$$
P(D|E)={0.6×0.05\over 0.0395}=0.76
$$
也就是说，对于检测结果为阳性的违禁药物使用者，大约有1/4的人是无辜的！

6.3 随机变量

随机变量（random variable）通常用实数表示概率事件。在之前的案例中，我们认为变量（在数学和程序语言中）是固定值。在数学中，我们可以用h表示直角三角形的斜边长。在Python中用x表示5（x=5）。以上两个变量每次只能是唯一值。但是，随机变量具有随机性，随机变量的值和它的名称一样是变化的，随环境而改变！

但是和变量一样，随机变量也用来存储值，两者最大的区别在于随机变量的取值具有不确定性，完全取决于所处的环境。

如果随机变量有多个取值，那我们如何追踪每个值呢？答案是随机变量的每个值都对应一个百分比。也就是说，对于随机变量可能出现的每一个值，都有唯一一个与之对应的概率。

我们可以计算出随机变量的概率分布，观察随机变量可能的取值和概率。我们通常用大写字母（经常用X）表示随机变量，比如：

  • X=掷骰子的结果。
  • Y=某公司今年的销售额。
  • Z=应聘者的编程测试得分。

事实上，随机变量是将样本空间（包含了所有可能的结果）中的值映射到概率（0~1）的函数，用公式表达如下：
$$
f(事件)=概率
$$
函数将给出每一个事件对应的概率。随机变量主要有两种类型：离散型（discrete）和连续型（continuous）。

6.3.1 离散型随机变量

离散型随机变量的取值范围是有限的，比如掷骰子的结果。
$$
X=每次掷骰子的结果
$$

随机变量值 X=1 X=2 X=3 X=4 X=5 X=6
概率 1/6 1/6 1/6 1/6 1/6 1/6

我们用大写X表示随机变量，这是随机变量最常见的符号，同时还需注意到每个随机变量都有一个与之对应的概率。

随机变量有很多属性，比如期望（expected value）和方差（variance）。我们通常用概率质量函数（probability mass function,PMF）描述离散随机变量的分布情况，表示方法如下：
$$
P(X=x)=PMF
$$
对于掷骰子事件：

P(X=1)=1/6，P(X=5)=1/6

对于以下两种离散型随机变量：

  • 调查问卷的结果（范围是1~10）
  • CEO是否会在年内辞职（非真即假）

随机变量的期望是指大量随机变量样本的平均值，有时也被称为变量的平均值。下面用Python代码模拟掷骰子事件。

1
2
3
4
import random
import matplotlib.pyplot as plt
def random_variable_of_dice_roll():
    return random.randint(1,7) #a range of (1,7) #includes 1,2,3,4,5,6,but NOT 7

下面我们掷100次骰子，观察其平均值的大小。

1
2
3
4
5
trials=[]
num_trials=100
for trial in range(num_trials):
    trials.append(random_variable_of_dice_roll())
print(sum(trials)/float(num_trials))  #==3.77

掷100次骰子后的平均值是3.77。下面增大掷骰子的次数。

1
2
3
4
5
6
7
8
9
10
11
num_trials=range(100,10000,10)
avgs=[]
for num_trial in num_trials:
    trials=[]
    for trial in range(1,num_trial):
        trials.append(random_variable_of_dice_roll())
    avgs.append(sum(trials)/float(num_trial))
plt.plot(num_trials,avgs)
plt.xlabel('Number of Trials')
plt.ylabel("Average")
plt.show()

image-20230326175807622

上图是掷骰子的次数和平均值之间的关系。图中左侧显示，如果掷骰子的次数只有100 次，那么很难保证平均值接近3.5。然而，如果连续掷10000次骰子，平均值明显越来越接近3.5。

对于离散型随机变量，我们用以下公式计算期望：
$$
期望=E[X]=μ_X=∑x_ip_i
$$
其中，$x_i$是第i次的结果，$p_i$是第i次的概率。

对于掷骰子事件，我们可以计算其期望为：
$$
{1\over 6}(1)+{1\over 6}(2)+{1\over 6}(3)+{1\over 6}(4)+{1\over 6}(5)+{1\over 6}(6)=3.5
$$
计算结果显示，我们每掷一次骰子，预期得到的值是3.5。然而，骰子并没有3.5，期望值好像是没有意义的！实际上，如果考虑到研究背景——掷很多次骰子，3.5就是有意义的数值。因为如果我们掷10000次骰子，骰子的平均点数确实接近3.5，图6.1就是最好的证明。

随机变量的期望并不能描述随机变量所有的特征，因此我们需要引入方差的概念。

方差用来描述随机变量的离散程度，它量化了变量值的不确定性。离散型随机变量的方差公式如下：
$$
方差=V[X]=σ^2_X=∑(x_i-μ_x)^2p_i
$$
其中，$x_i$和$p_i$，与之前的含义相同，$μ_x$是随机变量的期望。公式中还出现了西格玛σ，它是随机变量的标准差，等于方差的平方根。

方差可以被看作增减指标。假设有人告诉你可以从扑克比赛中赢得100美元，你会非常高兴。如果他继续说：“你可能赢得100美元，加减80美元。”那么你的预期回报将是100加减80，浮动范围非常广。这会让风险厌恶者慎重考虑是否需要加入比赛。

下面我们介绍更复杂的离散型随机变量案例。假设你的团队用李克特度量法（Likert Scale）评估新产品是否会成功，其中用0表示彻底失败，4表示获得巨大成功。你们根据新产品的用户测试结果和历史产品表现预测新产品的成功概率。

首先，我们需要定义随机变量。假设随机变量X表示产品成功情况，由于X的值只有5种可能：0、1、2、3或4，所以X是离散型随机变量。表6.3是X的概率分布。请注意，每一列代表随机变量可能的取值和它对应的概率。

随机变量值 X=0 X=1 X=2 X=3 X=4
概率 0.02 0.07 0.25 0.4 0.26

比如，该产品有2%的概率彻底失败，26%的概率获得巨大成功！我们可以计算X的期望：
$$
E[X]=0×(0.02)+1×(0.07)+2×(0.25)+3×(0.4)+4×(0.26)=2.81
$$
因此，管理层可以认为该产品成功的期望值是2.81。但是，仅有这个数字还不足以下结论。当我们有多个项目备选时，期望可能是较好的对比指标。然而，当我们仅有一个项目时，我们需要更多的衡量指标。

下面，我们将计算X的方差，如下：
$$
V[X]=(0-2.81)^2×0.02+(1-2.81)^2×0.07+(2-2.81)^2×0.25+(3-2.81)^2×0.4+(4-2.81)^2×0.26=0.97
$$
由此可知标准差等于0.97。

因此，我们可以认为新产品获得成功的期望是2.81加减0.97，即1.84~3.78。

你可能在想，好吧，这个新产品最好的得分是3.78，最差的得分是1.84。然而并不是这样！新产品既可能是4分，也可能低于1.8分。为了证明这一点，我们计算P(X≥3)。

P(X≥3)指随机变量值大于或等于3的概率。换句话说，新产品的得分大于或等于3的概率是多少？
$$
P(X≥3)=P(X=3)+P(X=4)=0.66=66%
$$
这意味着新产品有66%的概率得分是3或4。

另一种计算它的方式是根据共轭法则，如下：
$$
P(X≥3)=1-P(X<3)
$$
这个公式的意思是为了计算得分不低于3的概率，我们用1减去得分低于3的概率。只有当两个事件（X≥3和X<3）是互补事件时，它才成立。

P(X≥3)和P(X<3)显然是互补事件，因为产品得分只能是以下两种情况之一：

  • 等于或大于3。
  • 小于3。

我们还可以通过计算P(X<3)检查等式是否成立：
$$
P(X<3)=P(X=0)+P(X=1)+P(X=2)=0.02+0.07+0.25=0.34
\
1-P(X<3)=1-0.34=0.66=P(X≥3)
$$
这说明X≥3和X<3是互补事件。

排列组合公式

46b4eee6780276c8d107c99f84a7dee

二项随机变量

第一种离散型随机变量是二项随机变量（binomial random variables）。二项随机变量指重复观察某一试验，并统计试验结果为“成功（真）”的次数。

在学习二项随机变量之前，我们需要知道什么是二项分布。二项分布需要满足以下4个条件：

  • 试验结果只有两种：成功或失败（发生或不发生，真或假）；
  • 试验结果是独立的，互不影响的；
  • 试验次数的固定的（固定样本大小）；
  • 每次试验成功的概率均为p。

image-20230326192654522

二项分布：n次伯努利事件，发生r次的概率

$$
P(X=r)=C_n^r·p^r·(1-p)^{n-r}
$$

下面我们用一个视频来帮助我们理解二项分布。

视频地址：十分钟理解二项分布

8995fb365b2800719a6b0626802d930

a99c2329c0cc7820a61c5d69de6dc7e

案例：餐馆生存概率

已知某城市餐馆开业首年的生存率是20%。假设今年有14家餐馆开业，请问1年后有4家餐馆生存下来的概率是多少？

首先，我们需要验证这是一个二项分布试验：

  • 试验结果是餐馆继续营业或关门；

  • 试验结果是独立的，互不影响——假设各餐馆之间不影响对方的生存概率；

  • 试验次数是固定的——14家餐馆开业；

  • 每次试验成功的概率都为p——生存率是20%。

我们已经知道两个参数n=14，p=0.2，下面将参数填进公式，如下：
$$
P(X=4)=C_{14}^4×0.2^4×0.8^{10}=0.17
$$
因此，1年之后有4家餐馆继续营业的概率是17%。

案例：血型

假设某对夫妻孩子血型为O的概率是25%。请问在他们的5个孩子中，有3个血型为O的概率是多少？

我们用X表示孩子血型为O，其中n=5，p=0.25，那么：
$$
P(X=3)=C_5^3×0.25^3×0.75^{5-3}=0.087
$$
我们还可以计算随机变量值为0、1、2、3、4和5时对应的概率，了解它的概率分布。

随机变量值 0 1 2 3 4 5
概率 0.23730 0.39551 0.26367 0.08789 0.01465 0.00098

有了以上概率分布，我们就可以计算变量的期望和方差：
$$
期望=E[X]=μ_x=∑x_ip_i=1.25
\
方差=V[X]=σ^2_x=∑(x_i-μ_x)^2p_i=0.9375
$$
因此我们预计该家庭有1~2个孩子的血型为O型。

如果我们想知道至少有3个孩子血型为O型的概率是多少，我们可以使用以下公式：
$$
P(X≥3)=P(X=5)+P(X=4)+P(X=3)=0.00098+0.01465+0.08789=0.103
$$
因此，该家庭有3个小孩的血型为O型的概率是10%。

计算二项随机变量期望和方差的快捷方式如下。

二项随机变量有特殊的计算期望和方差的方法。如果X是二项随机变量，那么：

E[X]=np

V[X]=np(1-p)

对于上面的例子，我们可以使用以下公式计算期望和方差：

E[X]=0.25×5=1.25

V[X]=1.25×(0.75)=0.9375

二项随机变量是计算二项分布试验成功次数的离散型随机变量。它在数据驱动的实验中具有重要作用，比如在给定转化率的前提下预测注册人数，或者预测股票价格下跌的幅度（别着急，我们随后会用更强大的模型预测股票价格的变化）。

几何随机变量

第二种随机变量类型是几何随机变量（geometric random variables）。事实上，它和二项随机变量非常类似，适用的对象同样是重复发生的事件。两者的区别在于几何随机变量不再限制样本的大小。比如，对于之前的”血型”案例，我们不再限定只有5个孩子。相反，我们对试验的次数进行建模，计算第1次试验成功的概率。

一般情况下，几何分布的事件或试验需要满足以下4个条件：

  • 试验结果只有两种：成功或失败（发生或不发生，真或假）；
  • 试验结果是独立的，互不影响的；
  • 试验次数不固定；
  • 每次试验成功的概率均为p。

请注意，除了第3个条件之外，其他条件和二项随机变量完全一致！

几何随机变量属于离散型随机变量，它用于计算试验第一次成功的概率。参数p表示每次试验成功的概率，（1-p）是每次试验失败的概率。

几何随机变量的案例有：

  • 计算创业公司在得到第一笔风险投资前，需要和VC会面的次数；

  • 计算掷硬币时得到第1个正面朝上的投掷次数。

几何随机变量的概率质量函数（PMF）如下：
$$
P(X=x)=(1-p)^{x-1}p
$$
简单概括，二项分布和几何分布的结果都只能是成功或失败两种。两者最大的不同是二项随机变量有固定的次数（记为n），几何随机变量没有固定的试验次数。相反，几何随机变量对第1次试验成功的概率进行建模——不考虑成功的真实含义。

案例：天气

假设4月每一天降雨的概率都是34%。请问4月4号之前下雨的概率是多少？

根据已知条件，事件X是第1次降雨发生的日期，概率p等于0.34，(1-p)等于0.66，那么：
$$
P(X=8)=0.66^{8-1}×0.34=0.66^7×0.34=0.01855
$$
因此，4月4号之前下雨的概率等于：
$$
P(X≤4)=P(1)+P(2)+P(3)+P(4)=0.34+0.22+0.14+0.10=0.8
$$
因此，4月4号之前下雨的概率是80%。

计算几何型随机变量期望和方差的快捷方式如下。

几何随机变量同样有特殊的计算期望和方差的方法。如果X是几何型随机变量，那么：

E[X]=1/p

V[X]=(1-p)/$p^2$

泊松随机变量

第三种随机变量类型是泊松随机变量（poisson random variable）。泊松随机变量用于计算事件在特定时间段内发生的次数。假设根据历史数据，在某特定期间内，事件X 的平均发生次数是μ，那么泊松随机变量记为X=Poi(μ)。

泊松分布是离散型概率分布，以下是两个泊松随机变量案例：

  • 根据网站历史表现，预测在1小时内网站访问者数量达到特定值的概率；

  • 根据历史交通报告，预测某十字路口的车祸数量。

如果用X表示指定期间事件发生的次数，用λ表示给定期间内事件的平均发生次数，那么在给定期间内，事件发生x次的概率可以用以下公式表示：
$$
P(X=x)={e^{-λ}λ^x\over x!}
$$
其中，e是欧拉常数（2.718……）。

我们用一个视频来看看泊松随机变量是怎么来的。

视频地址：泊松分布是怎么来的？应该怎么用？

6221180e7115f36473cad04bddc24f2

0e8bd7343904086996b8f33618154d3

案例：呼叫中心

已知呼叫中心接到的电话数量服从泊松分布，平均每小时5个电话。请问：在晚上10点～11点接到6个电话的概率是多少？

求解该问题之前，我们先写下所有已知的信息，随机变量X指晚上10点～11点接到电话的数量，λ等于5。请注意，平均值5不是凭空瞎猜的，而是来自对过去这个时间段电话数量的分析。我们需要通过各种方法对平均值进行估计，以便生成泊松随机变量进行预测。

继续求解我们的问题：
$$
P(X=6)={e^{-5}5^6\over6!}=0.146
$$
因此，晚上10点~11点接到6个电话的概率是14.6%。

计算泊松随机变量期望和方差的快捷方式如下。

泊松随机变量同样有特殊的计算期望和方差的方法。如果X是泊松随机变量，那么：

E[X]=λ

V[X]=λ

6.3.2 连续型随机变量

image-20230327171717010

image-20230327171800339

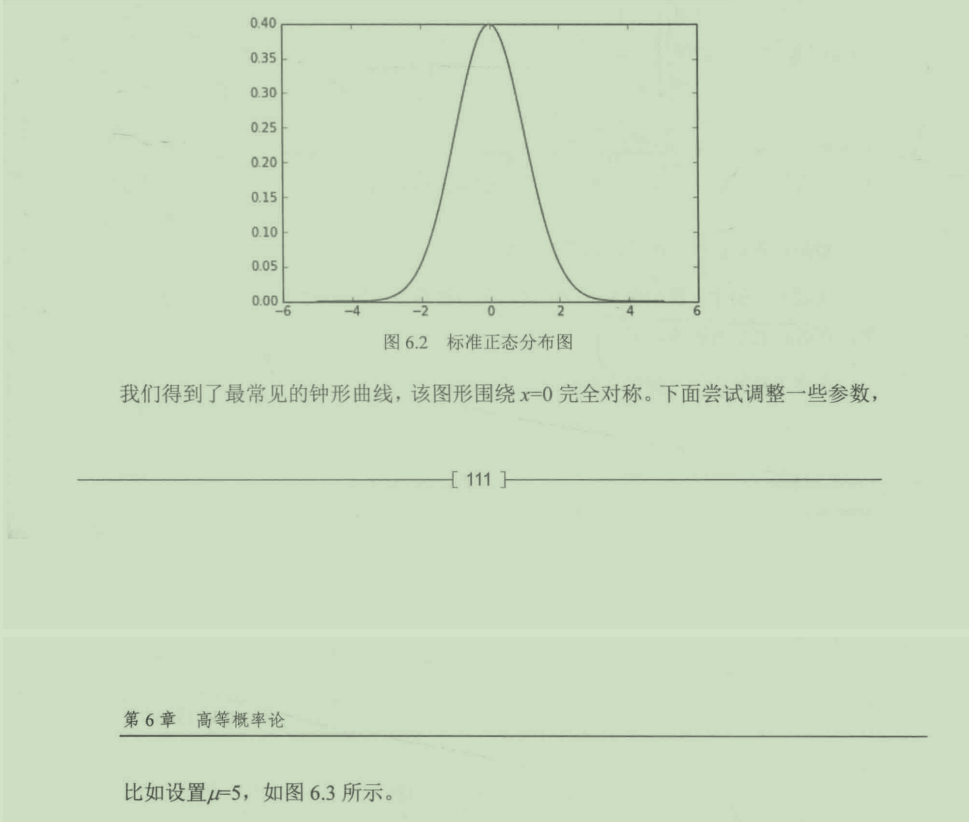
image-20230327171816564

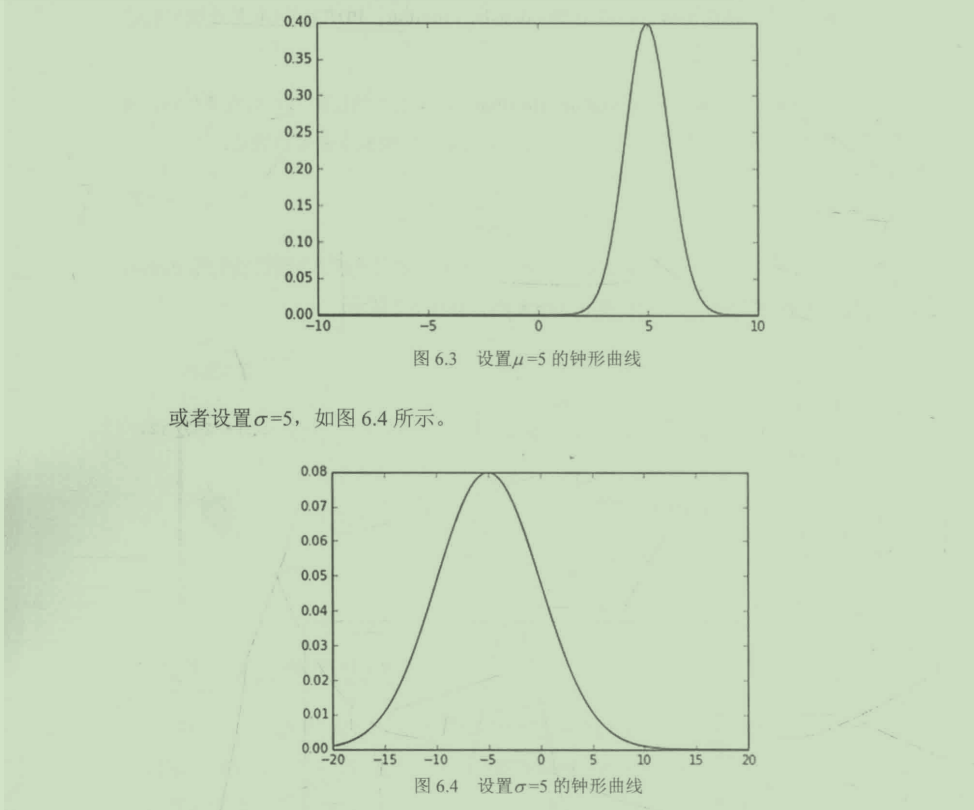
image-20230327171830966

image-20230327171848694

我们仍然可以通过一个视频来进一步了解连续型随机变量。

视频地址：【概率论与数理统计】一个视频让你明白分布函数，概率密度函数，分布律，联合概率密度，联合分布函数，联合分布律，边缘概率密度，边缘分布函数都是什么意义和概念