第5章 概率论入门：不可能，还是不太可能

[toc]

在接下来的几个章节中，我们将研究概率论和统计学，它们是现实世界中各种分析场景和数据驱动情景最常用的方法。概率论是预测的基础。我们用概率表示事件发生的可能性。通过概率论，我们能够对现实世界中某些随机性或偶发性事件进行建模。

5.1 基本的定义

概率论最基础的概念之一是过程（procedure）。过程指产生某个结果的行动。比如，掷骰子和访问网站。

事件（event）是某个过程产生的一系列结果的合集。比如，掷硬币得到正面朝上的结果或在网站停留4秒后离开。简单事件（simple event）指由某个过程产生的不可再分的事件。比如，掷两次骰子可以被拆分为以下两个简单事件：掷第1次骰子，掷第2次骰子。

样本空间（sample space）指某个过程产生的所有可能的简单事件的集合。比如，连续掷3次硬币，请问样本空间大小是多少？答案是8。因为实验结果只能是以下样本空间中的任何一个：{正正正，正正反，正反反，正反正，反反反，反反正，反正正，反正反}。

5.2 概率

事件的概率（probability）指事件出现的频率或可能性，A表示事件，P(A)表示事件发生的概率。我们定义事件A的概率为：
$$
P(A)={事件A出现的次数\over样本空间的大小}
$$
其中A是待求解的事件。

image-20230317141203456

首先我们定义事件A是两个正面朝上，A出现的次数有1次。事件的样本空间是{正在，正反，反正，反反}，样本空间大小是4。所以，事件A的概率P(A)等于1/4。

我们用一个交叉表对结果进行验证。第1枚硬币的结果用列表示，第2枚硬币的结果用行表示。每个单元格只能为“真”或“假”，其中“真”表示满足我们想要的结果（即两个正面朝上），“假”表示不满足。

第1枚硬币为正面 第1枚硬币为反面
第2枚硬币为正面 真 假
第2枚硬币为反面 假 假

可见，4个结果中只有1个满足要求。

5.3 贝叶斯VS频率论

上一个例子过于简单，因为在真实案例中，我们有时很难计算事件发生的次数。比如，随机抽取某个人，我们想知道他/她每天至少抽1次烟的概率。如果用传统的方式（概率公式）求解，我们需要知道烟民总数和每天至少抽1次烟的烟民数量分别是多少——这是不可能得到的数字！

面对这样的困境，在计算事件概率时出现了两个不同的方法：频率论方法（Frequentist approach）和贝叶斯论方法（Bayesian approach）。本章将重点研究频率论方法，下一章将重点研究贝叶斯方法。

频率论方法

在频率论方法中，事件的概率是通过实验获得的。它利用过去的数据预测未来某个事件的概率。频率论方法的公式如下：
$$
P(A)={事件A出现的次数\over过程被重复的次数}
$$
简而言之，我们观察事件的多个实例，计算事件A出现的次数，两者相除即为概率的近似值。

这和贝叶斯方法存在很大区别。贝叶斯方法更偏向通过理论方式计算事件的概率。我们需要更深入地思考事件本身和事件发生的原因。这两种方式计算的概率都不一定百分之百准确，选择何种方法取决于待解决的问题和计算难度。

频率论方法的核心是相对频率（relative frequency）。相对频率等于事件出现的次数除以总观测次数。

示例：营销统计

假设我们想知道网站用户中有多少人会再次访问，该指标被称为重复访客率（the rate of repeat visitors）。根据之前的公式，我们定义事件A为用户再次访问网站。接着，我们需要计算用户再次访问网站的方式有多少种，而这是没有意义的！因此在这个例子中，很多人倾向使用贝叶斯方法。然而，我们仍然可以用传统方法计算事件A的相对频率。

我们可以利用网站访问日志计算事件A的相对频率。假设过去1周，1458个独立访问者（unique visitors）中有452个人属于重复访问者（repeat visitors），那么：
$$
P(A)={452\over1458}=0.31
$$
因此，重复访客率大约是31%。

大数法则

大数法则（the law of large numbers）是频率论方法能够成立的原因。大数法则指如果我们不断重复某个过程，那么相对频率将接近真实概率。

如果我问你1~10的平均值是多少，你会脱口而出5。下面我们将用Python做实验，计算1~10的平均值，演示什么是大数法则。

我们通过Python从1~10中随机取n个数，并计算平均值，重复以上步骤，并逐渐增大n，最后用图表展示实验结果。具体实验步骤如下：

（1）从1~10取1个随机数，计算平均值；

（2）从1~10取2个随机数，计算平均值；

（3）从1~10取3个随机数，计算平均值；

（4）从1~10取10000个随机数，计算平均值；

（5）对以上结果绘图。

以下是实验代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
results=[]
for n in range(1,10000):
    nums=np.random.randint(low=1,high=10,size=n)
#choose n numbers between 1 and 10
    mean=nums.mean()       #find the average of these numbers
    results.append(mean)   #add the average to a running list
#POP QUIZ:How large is the list results?
len(results) #9999
#This was tricky because I took the range from 1 to 10000 and usually
#we do from 0 to 10000
df=pd.DataFrame({'means':results})
print(df.head()) #the averages in the beginning are all over the place!
#means
#9.0
#5.0
#6.0
#4.5
#4.0
print(df.tail()) #as n,our size of the sample size,increases,the
#averages get closer to 5!
#means
#4.998799
#5.060924
#4.990597
#5.008802
#4.979198
df.plot(title='Law of Large Numbers')
plt.xlabel("Number of throws in sample")
plt.ylabel("Average Of Sample")
plt.show()

image-20230318085001541

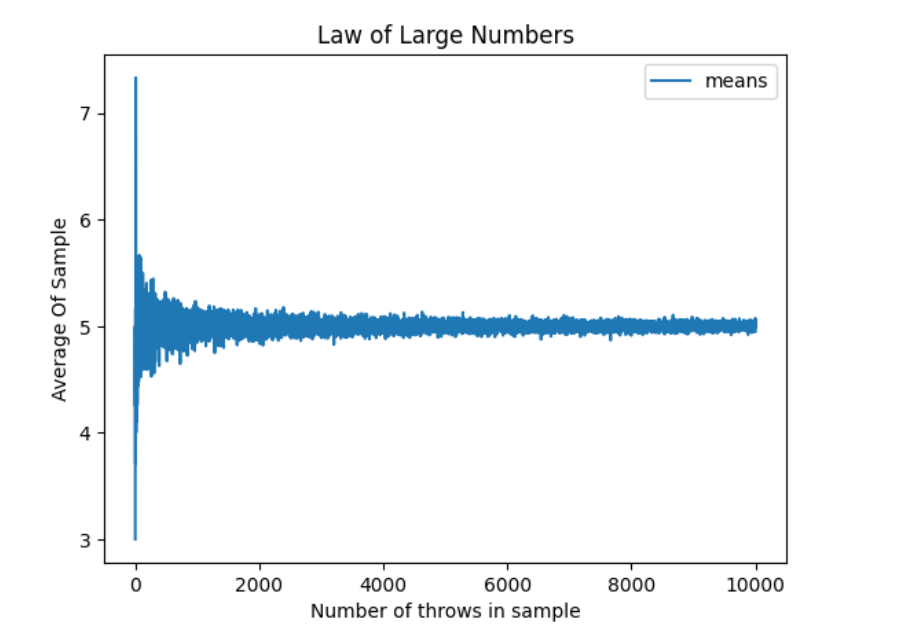
image-20230318085016896

如图所示，随着我们不断增加样本大小，相对频率逐渐接近真是平均值5。很酷，对吧？

在统计学章节，我们将给出更加严格的定义，现在你只需要知道大数法则可以让相对频率接近事件的真实概率。

5.4 复合事件

有时，我们需要同时处理两个或多个事件，这叫作复合事件（compound events）。复合事件指包含两个及以上简单事件的事件。

给定事件A和事件B：

  • 事件A和事件B同时发生的概率用Ｐ(A$\cap$B)=P(A且B)表示；
  • 事件A或事件B发生的概率用P(A$\cup$B)=P(A或B)表示。

深入理解为什么用集合（set）符号表示复合事件非常重要。还记得我们之前用大圆Universe表示全体事件吗？假设新开展一项关于癌症检测的实验，参与者有100人。

如图5.3所示，灰色区域A表示25名癌症患者。根据频率论方法，我们可以认为P(A)=癌症患者数/实验总参与人数，即25/100=1/4=0.25。也就是说，从100人中随机选取一人，患有癌症的概率是25%。

下面引入第2个事件B。事件B指癌症检测结果呈阳性（表示可能患有癌症）。假设事件B共有30人，所以P(B)=30/100=3/10=0.3。也就是说，从100人中随机选取一个，癌症检测结果为阳性的概率为30%，如图5.4所示。

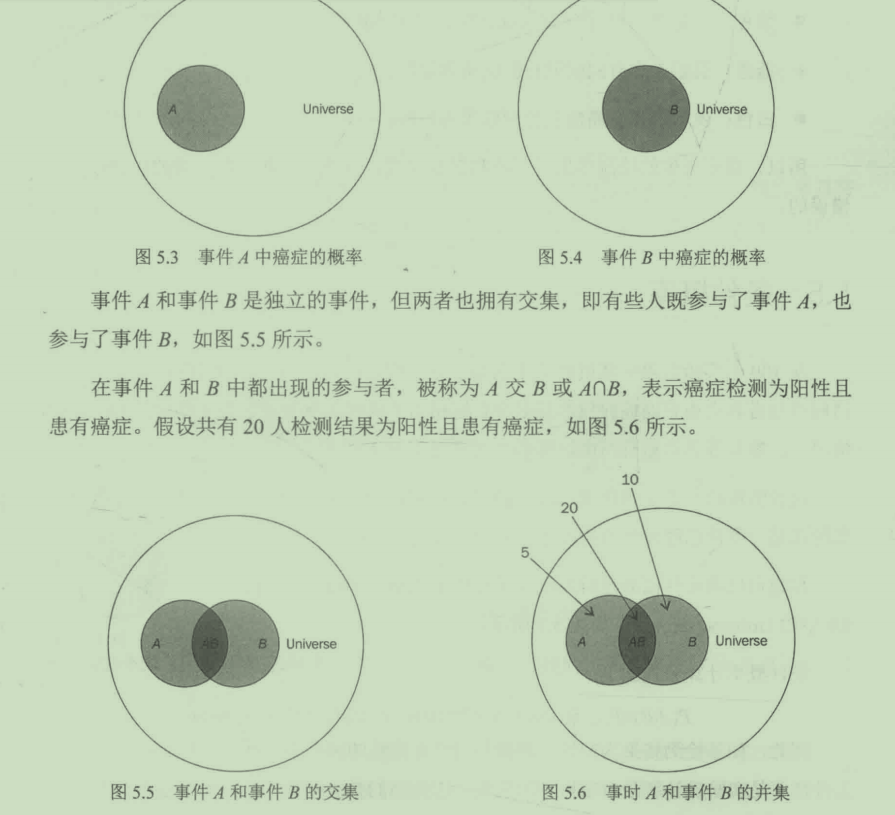
image-20230318091621197

这意味着P(A$\cap$B)=P(A且B)=20/100=1/5=0.2=20%。

如果想知道真实患有癌症或检测结果为阳性的概率，则只需要将两个事件相加，5+20+10=35，这些人要么是真实的癌症患者，要么癌症检测结果为阳性，P(A$\cup$B)=P(A或B)=35/100=0.35=35%

image-20230318093552471

简单总结，在上图中，实验的所有参与者有以下4种分类：

  • 粉色：表示患有癌症且检测结果为阴性
  • 紫色(A交B)：表示患有癌症且检测结果为阳性
  • 蓝色：表示未患有癌症但检测结果为阳性
  • 白色：表示未患有癌症且检测结果为阴性

所以，真正正确的检测结果是白色和紫色区域。

5.5 条件概率

从100名实验对象中随机挑选1名参与者。假设已知该参与者的检测结果为阳性，请问参与者真实患有癌症的概率是多少？这相当于求解在事件B已发生即结果为阳性的情况下，参与者真实患有癌症的概率，会不会是P(A)呢？

这种情况叫作给定条件B，求A的条件概率，记为P(A|B)。简而言之，条件概率是求解在某一事件已经发生的情况下，另一事件发生的概率。

你也可以将条件概率理解为改变了总体的大小。P(A|B)的总体由图5.6中的Universe变为B，如下图所示：

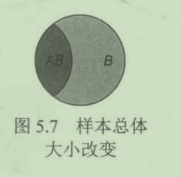
image-20230318101831390

条件概率计算公式如下：
$$
P(A|B)=P(A且B)/P(B)=P(A \cap B)/P(B)=(20/100)/(30/100)=2/3=66%
$$

用样本空间的改变来理解条件概率会非常有帮助。

P(A|B)的含义是，在B已经发生的条件下，A发生的概率。那么样本空间变为图5.7所示就很好理解。再根据最基础的公式不难得出P(A|B)=P(A $\cap$ B)/P(B)

因此，如果检测结果为阳性，则参与者患有癌症的概率为66%。在现实中，类似的条件概率是实验设计者最希望得到的结果，因为他们希望知道的是检测方法在预测癌症方面的真实效果。

5.6 概率定理

在概率论中，有一些难以可视化表达但非常有用的定理，这些定理将帮助我们轻松地计算复合概率。

5.6.1 加法定理

加法定理用于计算“或”事件的概率。我们可以通过以下公式计算P(A或B)即P(A $\cup$ B)的概率：
$$
P(A \cup B)=P(A)+P(B)-P(A \cap B)
$$
image-20230318103652766

回忆之前的案例，我们希望知道实验对象患有癌症或者检测结果为阳性的概率。假设事件A表示患有癌症，事件B表示检测结果为阳性。根据公式我们有：
$$
P(A \cup B)=P(A)+P(B)-P(A \cap B)＝0.25+0.30-0.2=0.35
$$
结果和我们之前计算的一样。

5.6.2 互斥性

当两个事件不能同时发生时，我们称它们为互斥事件（mutually exclusive）。这意味着两个事件的交集为空集，即A$\cap$B=Ø,或P(A$\cap$B)=P(A且B)=0。

如果两个事件是互斥的，那么：
$$
P(A \cup B)=P(A或B)=P(A)+P(B)-P(A \cap B)=P(A)+P(B)
$$
以下是常见的互斥事件：

  • 用户通过Twitter和用户通过Facebook登录你的网站；
  • 今天是星期六和今天是星期三；
  • 未通过经济学101课和已通过经济学101课。

以上案例中的事件不可能同时发生。

5.6.3 乘法定理

乘法定理用于计算“且”事件的概率。我们可以通过以下公式计算P(A$\cap$B)即P(A且B)：
$$
P(A \cap B)=P(A且B)=P(A)·P(B|A)
$$
为什么是乘以P(B|A)而不是P(B)呢？这是因为P(A)和P(B)相乘不能适用于所有情况，比如事件B可能依赖于事件A。

回到癌症实验案例中，假设A表示检测结果为阳性，B表示患有癌症。根据公式我们有：
$$
P(A \cap B)=P(A且B)=P(A)·P(B|A)=0.3×0.6666=0.2=20%
$$
结果和我们之前计算的一样。

下面是公式推导过程，能帮助我们理解乘法定理。

image-20230320145325424

你也许还没有认识到条件概率的必要性。下面让我们看另一个更难的案例。

假设随机选取10人，有6人使用iPhone，4人使用Android。请问随机选取两个人都使用iPhone的概率是多少？也就是说，对于以下两个事件：

  • 事件A：第1个人使用iPhone。
  • 事件B：第2个人使用iPhone。

求P(A且B)，即P(iPhone用户且iPhone用户)的值。

我们可以使用公式P(A且B)=P(A)·P(B|A)。

P(A)很容易计算，10个人中有6个是iPhone用户，所以事件A发生的概率是6/10=3/5=0.6。即P(A)=0.6。如果选取1个iPhone用户的概率是0.6，那么选取2个iPhone用户的概率应该是0.6×0.6对吧？

等等！在选取第2个iPhone用户时，只剩下了9个人。所以在转换后的样本空间中，我们有9个人，其中5个是iPhone用户，4个是Android用户，因此P(B|A)=5/9=0.555。

因此，选取两个人都使用iPhone的概率是0.6×0.555=0.333=33%。即从10个人中随机选取两个人使用iPhone的概率是1/3。

总之，条件概率的乘法定理非常重要，有时它会彻底改变你的计算结果。

5.6.4 独立性

如果两个事件互不影响对方的发生，那么这两个事件是相互独立的，因此：
$$
P(B|A)=P(B),P(A|B)=P(A)
$$
如果两个事件是独立事件，那么：
$$
P(A \cap B)=P(A)·P(B|A)=P(A)·P(B)
$$
以下是常见的独立事件：

  • 旧金山在下雨，同时一个婴儿在印度出生；
  • 抛第1枚硬币得到正面，抛第2枚硬币得到反面。

以上案例中的事件属于独立事件，它们互不影响对方的发生概率。

5.6.5 互补事件

事件A的互补事件（complementary events）指事件A的相反事件或否定事件，通常用Ā表示。比如，如果事件A表示某人患有癌症，则Ā表示某人未患有癌症。

我们通常用以下公式计算Ā的概率：
$$
P(Ā)=1-P(A)
$$
比如，假设投掷两次骰子，请问得到的值大于3的概率是多少？如果用A表示值大于3，Ā表示值等于或小于3，则：
$$
P(A)=1-P(Ā)
\
P(A)=1-(P(2)+P(3))
\
\quad\quad\quad=1-(1/36+2/36)
\
=1-(3/36)
\
=33/36
\
=0.91
$$
再比如，某创业团队马上要和3个不同的投资者开会，我们已知以下概率：

  • 第1场会议获得投资的概率是60%
  • 第2场会议获得投资的概率是15%
  • 第3场会议获得投资的概率是45%

请问，这个团队至少获得1笔投资的概率是多少？

用A表示至少获得１笔投资，Ā表示没有获得任何投资，则P(A)可以用以下公式表示：
$$
P(A)=1-P(Ā)
$$
为了计算P(Ā)，我们需要计算以下概率：

P(Ā)=P(没有拿到第1个投资者的投资 且 没有拿到第2个投资者的投资 且 没有拿到第3个投资者的投资)。

我们假设这些事件是独立事件（投资者间没有互相交流），那么：

P(Ā)=P(没有拿到第1个投资者的投资)×P(没有拿到第2个投资者的投资)×P(没有拿到第3个投资者的投资)=0.4×0.85×0.55=0.187
$$
P(A)=1-0.187=0.813=81%
$$
所以，这个创业团队至少拿到一笔投资的概率是81%。

5.7 再进一步

下面这个测试叫作二元分类器（binary classifer），它来自机器学习。你暂时不需要了解机器学习，只需要知道这个二元分类器只能预测两种结果：癌症和非癌症。当我们使用二元分类器时，可以计算出模型的混淆矩阵（confusion matrix）。这是一个2×2矩阵，每个单元格表示实验可能出现的结果之一。

我们换一组实验数据。假设有165人参与了实验，我们已经通过其他途径知道他们是否真正患有癌症。以下是实验结果的混淆矩阵。

n=165 模型预测结果：无癌症 模型预测结果：癌症
实际情况：无癌症 50 10
实际情况：癌症 5 100

矩阵显示，分类器预测50人没有得癌症，实际上他们确实不是癌症患者：有100人患有癌症，实际上他们确实是癌症患者。也就是说，我们得到了以下4个不同的分类。

  • 真阳性（true positives）：指分类器正确预测了癌症（阳性），共100人。
  • 真阴性（true negatives）：指分类器正确预测了非癌症（阴性），共50人。
  • 假阳性（false positive）：指分类器错误地预测了癌症（阳性），共10人。
  • 假阴性（false negatives）：指分类器错误地预测了非癌症（阴性），共5人。

前两类预测结果正确，后两类预测结果错误。假阳性被称为Ⅰ型错误（type Ⅰ error），假阴性被称为Ⅱ型错误（type Ⅱ error）。

我们将在后面的章节继续讨论这件事。现在，你只需要知道为什么我们使用集合符合表示复合事件的概率——交集表示事件A和事件B同时发生，并集表示事件A和事件B至少有一个发生。

image-20230321224331520

Ⅰ型错误是将没有患病的人错误诊断成患病，Ⅱ型错误是将患病的人错误诊断成没有患病。

从造成的后果上来说，Ⅱ型错误更加危险。